题目内容
6.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,求∠E1D1B的度数.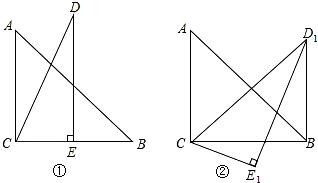
分析 先根据已知条件得:△D1CE1各角的度数,由旋转得:∠BCE1=15°,证明△ABC≌△CBD1,可以得出结论.
解答 解:由题意得:∠CD1E1=∠D=30°,∠D1CE1=∠DCE=90°-30°=60°,
∵把△DCE绕点C顺时针旋转15°得到△D1CE1,
∴∠BCE1=15°,
∴∠D1CB=60°-15°=45°,
在△ACB和△CBD1中,
∵$\left\{\begin{array}{l}{AB=C{D}_{1}}\\{∠ABC=∠{D}_{1}CB}\\{CB=BC}\end{array}\right.$,
∴△ABC≌△CBD1,
∴∠CD1B=∠A=45°,
∴∠E1D1B=∠CD1B-∠CD1E1=45°-30°=15°.
点评 本题考查了旋转的性质和三角形全等的判定和性质,根据图形准确找出△ABC≌△CBD1是本题的关键,注意字母的书写.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列函数是二次函数的是( )
| A. | y=2x+2 | B. | y=-2x | C. | y=x2+2 | D. | y=x-2 |
14.关于x的方程(a-3)x|a|-2+3=0是一元一次方程,则a的值是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 以上都不正确 |
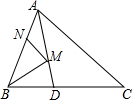 △ABC中,AB=13,BC=20,AC=21,AD平分∠BAC,M、N分别是AD、AB上的点,则BM+MN的最小值是12.
△ABC中,AB=13,BC=20,AC=21,AD平分∠BAC,M、N分别是AD、AB上的点,则BM+MN的最小值是12.
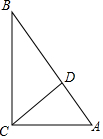 在Rt△ABC中,∠C=90°,由下列条件解直角三角形:
在Rt△ABC中,∠C=90°,由下列条件解直角三角形: