题目内容
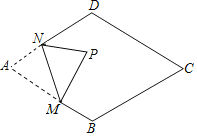
【题目】如图,在菱形ABCD中,∠A=60°,AB=6,点M为AB边上一点,AM=4,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为_____.
【答案】4或10﹣2![]() .
.
【解析】
分两种情况:①当点![]() 在菱形对角线
在菱形对角线![]() 上时,由折叠的性质得:
上时,由折叠的性质得:![]() ,
,![]() ,证出
,证出![]() ,得出
,得出![]() ;
;
②当点![]() 在菱形对角线
在菱形对角线![]() 上时,设
上时,设![]() ,由折叠的性质得:
,由折叠的性质得:![]() ,
,![]() ,
,![]() ,求出
,求出![]() ,证明
,证明![]() ,得出比例线段
,得出比例线段![]() ,可求出答案
,可求出答案
解:分两种情况:①当点P在菱形对角线AC上时,如图1所示:
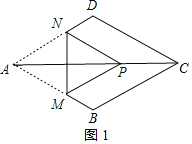
由折叠的性质得:AN=PN,AM=PM,
∵四边形ABCD是菱形,∠BAD=60°,
∴∠PAM=∠PAN=30°,
∴∠AMN=∠ANM=90°﹣30°=60°,
∴AN=AM=4;
②当点P在菱形对角线BD上时,如图2所示:
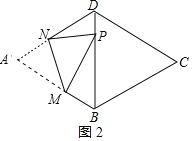
设AN=x,
由折叠的性质得:PM=AM=4,PN=AN=x,∠MPN=∠A=60°,
∵AB=6,
∴BM=AB﹣AM=2,
∵四边形ABCD是菱形,
![]() ,
,![]() ,
,
∵∠BPN=∠BPM+60°=∠DNP+60°,
∴∠BPM=∠DNP,
∴△PDN∽△MBP,
![]()
![]() ,即
,即![]() ,
,
![]() ,
,
![]()
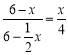 ,
,
解得:![]() 或
或![]() (不合题意舍去),
(不合题意舍去),
综上所述,![]() 的长为4或
的长为4或![]() .
.
故答案为:4或![]() .
.

 考前必练系列答案
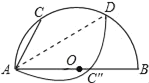
考前必练系列答案【题目】如图,以![]() 为直径的半圆上有一点
为直径的半圆上有一点![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上一个动点,连接
上一个动点,连接![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交半圆于点
,交半圆于点![]() .已知:
.已知:![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() ).
).
小青同学根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 变化而变化的规律进行了探究.
变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值,请补全表格;
的几组对应值,请补全表格;
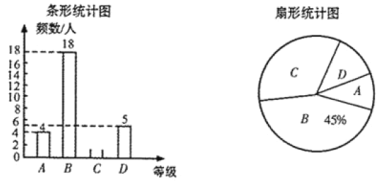
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| 5 | 2.85 | 1.98 | 1.52 | 1.21 | 0.97 | 0.76 | 0.56 | 0.37 | 0.19 | 0 |
| 0 | 0.46 | 1.29 | 1.61 | 1.84 | 1.96 | 1.95 | 1.79 | 1.41 | 0 |
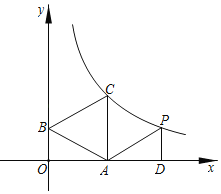
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
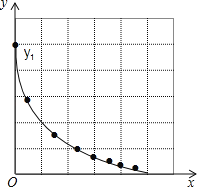
(3)结合函数图象,解决问题:
①当![]() ,
,![]() 的长都大于
的长都大于![]() 时,
时,![]() 长度的取值范围约是 ;
长度的取值范围约是 ;
②点![]() ,
,![]() ,
,![]() 能否在以
能否在以![]() 为圆心的同一个圆上? (填“能”或“否”)
为圆心的同一个圆上? (填“能”或“否”)