题目内容
已知正比例函数f（x）=kx（k＜0），用“＜““＞“符号连接：f（-1）
＞
＞
f（1）．分析：先根据k＜0判断出函数的增减性，再根据-1＜1即可作出判断．
解答：解：∵正比例函数f（x）=kx中，k＜0，
∴f（x）随x的增大而减小，
∵-1＜1，
∴f（-1）＞f（1）．
故答案为：＞．
∴f（x）随x的增大而减小，
∵-1＜1，
∴f（-1）＞f（1）．
故答案为：＞．
点评：本题考查的是一次函数图象上点的坐标特点，即一次函数图象上各点的坐标一定适合此函数的解析式
练习册系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
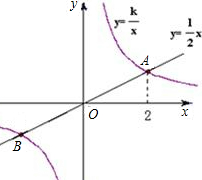横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．