题目内容
在一个暗箱中装有红、黄、自三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是 .
.
(1)求暗箱中红球的个数.
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树状图或列表法求解)
(1)1;(2) .
.
【解析】
试题分析:(1)设红球有x个,根据概率的意义列式计算即可得解;
(2)画出树状图,然后根据概率公式列式计算即可得解.
试题解析:(1)设红球有x个,
根据题意得,
 ,
,
解得x=1;
(2)根据题意画出树状图如下:

一共有9种情况,两次摸到的球颜色不同的有6种情况,
所以,P(两次摸到的球颜色不同)= .
.
考点:1.列表法与树状图法;2.概率公式.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目


 向上平移2个单位后,得到的函数表达式是( )
向上平移2个单位后,得到的函数表达式是( ) B.
B. C.
C. D.
D.

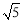 B.3
B.3 +6x+k=0的两个根分别是
+6x+k=0的两个根分别是 ,且
,且 ,则k的值为___________.
,则k的值为___________. ,那么AB等于( )
,那么AB等于( )
