Question

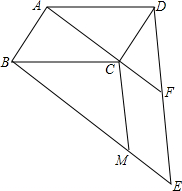已知如图，四边形ABCD为平行四边形，AD=a，AC为对角线，BM∥AC，过点D作 DE∥CM，交AC的延长线于F，交BM的延长线于E．
（1）求证：△ADF≌△BCM；
（2）若AC=2CF，∠ADC=60°，AC⊥DC，求四边形ABED的面积（用含a的代数式表示）．

Answer 1

分析：（1）由平行线的性质可得∠BMC=∠AFD，∠FAD=∠MBC，进而可得出结论．
（2）可把四边形ABED的面积分解为△ADF的面积与四边形ABEF的面积进行求解．

解答：（1）证明：在平行四边形ABCD中，则AD=BC，
∵AC∥BM，∴∠AFD=∠E，
又CM∥DE，∴∠BMC=∠E，
∴∠BMC=∠AFD，
同理∠FAD=∠MBC，
则在△ADF与△BCM中．

∠BMC=∠AFD ∠FAD=∠MBC AD=BC

，
∴△ADF≌△BCM．
（2）解：在△ACD中，
∵AC⊥CD，∠ADC=60°，
∴CD=

1

2

AD=

1

2

a，
则AC=

3

2

a，AF=

3 3

4

a，
又由（1）可得BE=

3

a，
S_ABED=S_△ADF+S_ABEF=

1

2

•AF•CD+

1

2

（AF+BE）•CD=

1

2

×

3 3

4

a×

1

2

a+

1

2

（

3 3

4

a+

3

a）×

1

2

a=

5 3

8

a²．

点评：本题主要考查了平行四边形的性质，全等三角形的判定及性质以及三角形，四边形面积的求法，应熟练掌握．