题目内容
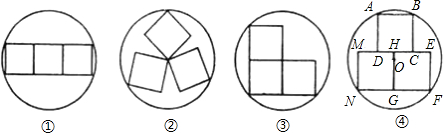
22、（A类）已知如图，四边形ABCD中，AB=BC，AD=CD，求证：∠A=∠C．（B类）已知如图，四边形ABCD中，AB=BC，∠A=∠C，求证：AD=CD．
分析：（A）连接BD，根据SSS证明△ABC≌△CBD，即可得到∠A=∠C．
（B）连接AC，根据等边对等角得到∠BAC=∠BCA，因为∠A=∠C，则可以得到∠CAD=∠ACD，根据等角对等边可得到AD=DC．
（B）连接AC，根据等边对等角得到∠BAC=∠BCA，因为∠A=∠C，则可以得到∠CAD=∠ACD，根据等角对等边可得到AD=DC．
解答：
证明：如图，（A）连接BD，
∵AB=BC，AD=CD，
又∵BD=BD，
∴△ABD≌△CBD，
∴∠A=∠C；
（B）连接AC，
∵AB=BC，
∴∠BAC=∠BCA．
∵∠BAD=∠BCD，
∴∠CAD=∠ACD．
∴AD=CD．
证明：如图，（A）连接BD，∵AB=BC，AD=CD，
又∵BD=BD，
∴△ABD≌△CBD，
∴∠A=∠C；
（B）连接AC，
∵AB=BC，
∴∠BAC=∠BCA．
∵∠BAD=∠BCD，
∴∠CAD=∠ACD．
∴AD=CD．
点评：一题多解可以锻炼同学们的创新、求异思维能力．增加题目的“含金量”．此题还有更简便的解法，就是证全等，然后再用全等性质证边角相等．
练习册系列答案
相关题目
某区共有甲、乙、丙三所高中，所有高二学生参加了一次数学测试．老师们对其中的一道题进行了分析，把每个学生的解答情况归结为下列四类情况之一：A--概念错误；B--计算错误；C--解答基本正确，但不完整；D--解答
完全正确．各校出现这四类情况的人数分别占本校高二学生数的百分比如下表所示．
已知甲校高二有400名学生，这三所学校高二学生人数的扇形统计图如图．
根据以上信息，解答下列问题：
（1）求全区高二学生总数；
（2）求全区解答完全正确的学生数占全区高二学生总数的百分比m（精确到0.01%）；
（3）请你对表中三校的数据进行对比分析，给丙校高二数学老师提一个值得关注的问题，并说明理由．
完全正确．各校出现这四类情况的人数分别占本校高二学生数的百分比如下表所示．| A | B | C | D | |
| 甲校（%） | 2.75 | 16.25 | 60.75 | 20.25 |
| 乙校（%） | 3.75 | 22.50 | 41.25 | 32.50 |
| 丙校（%） | 12.50 | 6.25 | 22.50 | 58.75 |
根据以上信息，解答下列问题：
（1）求全区高二学生总数；
（2）求全区解答完全正确的学生数占全区高二学生总数的百分比m（精确到0.01%）；
（3）请你对表中三校的数据进行对比分析，给丙校高二数学老师提一个值得关注的问题，并说明理由．
（2013•下关区一模）甲、乙、丙三所学校进行了一次八年级数学联合考试．老师们对其中的一道题进行了分析，把每个学生的解答情况归结为下列四种情况之一：A～概念错误；B～计算错误；C～解答基本正确，但不完整；D～解答完全正确．
探究题