题目内容
已知二次函数y=-x2+bx+c中的函数y与自变量x之间的部分对应值如下表所示，点A（x1，y1），B（x2，y2）在该函数的图象上．当0＜x1＜1，2＜x2＜3时，y1与y2的大小关系是 ．
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -1 | 2 | 3 | 2 | -1 | … |
考点：二次函数图象上点的坐标特征
专题：
分析：根据表格数据判断出对称轴为直线x=2，再根据二次项系数小于0判断出函数图象开口向下，然后根据x的取值范围写出大小关系即可．
解答：解：由表可知，抛物线的对称轴为直线x=2，
∵a=-1＜0，
∴函数图象开口向下，
∵0＜x1＜1，2＜x2＜3，
∴y1＜y2．
故答案为：y1＜y2．
∵a=-1＜0，
∴函数图象开口向下，
∵0＜x1＜1，2＜x2＜3，
∴y1＜y2．
故答案为：y1＜y2．
点评：本题考查了二次函数图象上点的坐标特征，判断出对称轴和开口方向是解题的关键．
练习册系列答案
相关题目
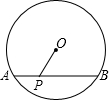如图，⊙O的直径为10，弦AB的长为8，P为弦AB上不同于A，B的一点．若OP的长为整数，则满足条件的点P有（ ）| A、2个 | B、3个 | C、4个 | D、5个 |