题目内容
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC.

(1)求证:AC是⊙O的切线:(2)若BF=8,DF= ,求⊙O的半径r.
,求⊙O的半径r.
(1)、略;(2)、6.
【解析】
试题分析:(1)、连接OA,OD,根据D为中点可得∠BOD=∠DOF=90°,∴∠D+∠OFD=90°,根据AC=FC得到∠FAC=∠AFC=∠OFD,根据OA=OD可得∠OAF=∠D,从而说明∠OAC=90°,得到切线;(2)、设OD=r,则OF=8-r,根据Rt△DOF的勾股定理求出r的值,然后根据OF的长度进行验根.
试题解析:(1)连结OA、OD,∵D为下半圆BE的中点,

∴∠BOD=∠DOF=90°,∴∠D+∠OFD=90°, ∵AC=FC,OA=OD,
∴∠CAF=∠CFA,∠OAD=∠D,∵∠CFA=∠OFD, ∴∠OAD+∠CAF=90°,∴OA⊥AC,∵OA为半径,
∴AC是⊙O的切线;
(2)∵⊙O半径是r,∴OD=r,OF=8﹣r,
又∵在Rt△DOF中,OD2+OF2=DF2,∴ ,解得,
,解得, ,
, ,
,
当 时,OF=
时,OF= (符合题意), 当
(符合题意), 当 时,OF=
时,OF= (不合题意,舍去),
(不合题意,舍去),
∴⊙O的半径r为6
考点:切线的判定、勾股定理.

练习册系列答案
相关题目
 满足
满足 ,则∠A= .
,则∠A= . 上的一个动点,且∠OPB=30°.设P点坐标为(m,n).
上的一个动点,且∠OPB=30°.设P点坐标为(m,n).
 ,求m的值;
,求m的值;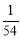 B.
B.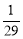 C.
C.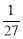 D.
D.

 的一个根,则a= .
的一个根,则a= .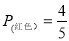 ,请你帮小明算一算,应该加入多少个红色的小球?
,请你帮小明算一算,应该加入多少个红色的小球? 