题目内容
16. 如图,在△ABC中,BC=2,∠A=70°,以BC边为直径作⊙O,分别交AB,AC于点D,E,连接DO,EO,则S扇形OBD+S扇形OEC=$\frac{7}{18}$π.(结果用π表示)
如图,在△ABC中,BC=2,∠A=70°,以BC边为直径作⊙O,分别交AB,AC于点D,E,连接DO,EO,则S扇形OBD+S扇形OEC=$\frac{7}{18}$π.(结果用π表示)
分析 先连接BE,根据圆周角定理可知∠AEB=90°,再由直角三角形的性质求出ABE的度数,由圆周角定理即可得出∠DOE的度数,最后根据∠DOB与∠COE的度数之和,求得S扇形OBD+S扇形OEC的值.
解答 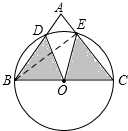 解:连接BE,
解:连接BE,
∵BC是直径,
∴AC⊥BE,
∴∠ABE=90°-∠A=20°,
∴∠DOE=2∠ABE=40°,
∴∠DOB+∠COE=140°,
又∵两个扇形的半径都是1,
∴S扇形OBD+S扇形OEC=$\frac{140×π×{1}^{2}}{360}$=$\frac{7}{18}$π.
故答案为:$\frac{7}{18}$π.
点评 本题主要考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
6.下列各数中,比1小的是( )
| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{3}{4}$ | D. | π |
1. 某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
(1)样本容量为150,表格c的值为0.26,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数为598;
(3)根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
 某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数为598;
(3)根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
