Question

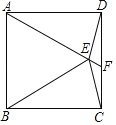
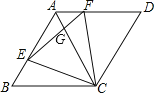
【题目】如图，菱形ABCD的边长为4，E，F分别是AB，AD边上的动点，BE＝AF，∠BAD＝120°，则下列结论：①△BEC≌△AFC；②△ECF为等边三角形；③∠AGE＝∠AFC；④若AF＝1，则． 其中正确结论的序号有________．

Answer 1

【答案】①②③④

【解析】

①易证△ABC为等边三角形，得AC=BC，∠CAF=∠B，结合已知条件BE=AF可证△BEC≌△AFC；②得FC=EC，∠FCA=∠ECB，得∠FCE=∠ACB，进而可得结论；③证明∠AGE=∠BFC则可得结论；④分别证明△AEG∽△FCG和△FCG∽△ACF即可得出结论．

在四边形是菱形中，

∵，

∴

∵

∴

∴△ABC为等边三角形，

∴

又，

∴，故①正确；

∴，

∴∠FCE=∠ACB=60°,

∴为等边三角形，故②正确；

∵∠AGE+∠GAE+∠AEG=180°，∠BEC+∠CEF+∠AEG=180°，

又∵∠CEF=∠CAB=60°,

∴∠BEC=∠AGE，

由①得，∠AFC=∠BEC，

∴∠AGE=∠AFC，故③正确；

∴∠AEG=∠FCG

∴△AEG∽△FCG，

∴，

∵∠AGE=∠FGC，∠AEG=∠FCG

∴∠CFG=∠GAE=∠FAC，

∴△ACF∽△FCG，

∴

∴

∵AF=1，

∴BE=1，

∴AE=3，

∴，故④正确．

故答案为：①②③④．