题目内容
（2001•安徽）⊙O1、⊙O2和⊙O3是三个半径为1的等圆，且圆心在同一条直线上．若⊙O2分别与⊙O1，⊙O3相交，⊙O1与⊙O3不相交，则⊙O1与⊙O3的圆心距d的取值范围是 ．
【答案】分析：三个等圆，其位置关系只可能是外离、外切、相交．根据题意，画出图形，再判断圆心距d的取值范围．
解答：解：两圆相交时，圆心距介于两圆半径的差与和之间，
则⊙O2与⊙O1的圆心距小于2，⊙O2与⊙O3的圆心距小于2，
又，⊙O1与⊙O3不相交，只可能外切或外离，即d≥2，
∴⊙O1与⊙O3的圆心距d的取值范围是2≤d＜4．
点评：本题利用了两圆相交时，圆心距介于两圆半径的差与和之间的性质求解．
解答：解：两圆相交时，圆心距介于两圆半径的差与和之间，
则⊙O2与⊙O1的圆心距小于2，⊙O2与⊙O3的圆心距小于2，
又，⊙O1与⊙O3不相交，只可能外切或外离，即d≥2，
∴⊙O1与⊙O3的圆心距d的取值范围是2≤d＜4．
点评：本题利用了两圆相交时，圆心距介于两圆半径的差与和之间的性质求解．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
（2001•安徽）某工厂生产的A种产品，它的成本是2元，售价是3元，年销量为100万件，为了获得更好的效益，厂家准备拿出一定的资金做广告；根据统计，每年投入的广告费是x（十万元），产品的年销量将是原销售量的y倍，且y是x的二次函数，它们的关系如表：
（1）求y与x的函数关系式；
（2）如果把利润看成销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费x（十万元的函数关系式）；
（3）如果投入的年广告费为10万元～30万元，问广告费在什么范围内，工厂获得的利润最大？最大利润是多少？
| x（十万元） | 1 | 2 | |
| y | 1 | 1.5 | 1.8 |
（2）如果把利润看成销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费x（十万元的函数关系式）；
（3）如果投入的年广告费为10万元～30万元，问广告费在什么范围内，工厂获得的利润最大？最大利润是多少？
（2001•安徽）某工厂生产的A种产品，它的成本是2元，售价是3元，年销量为100万件，为了获得更好的效益，厂家准备拿出一定的资金做广告；根据统计，每年投入的广告费是x（十万元），产品的年销量将是原销售量的y倍，且y是x的二次函数，它们的关系如表：
（1）求y与x的函数关系式；
（2）如果把利润看成销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费x（十万元的函数关系式）；
（3）如果投入的年广告费为10万元～30万元，问广告费在什么范围内，工厂获得的利润最大？最大利润是多少？
| x（十万元） | 1 | 2 | |
| y | 1 | 1.5 | 1.8 |
（2）如果把利润看成销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费x（十万元的函数关系式）；
（3）如果投入的年广告费为10万元～30万元，问广告费在什么范围内，工厂获得的利润最大？最大利润是多少？
=（ ）
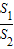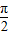
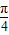
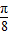
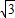≈1.73）