题目内容
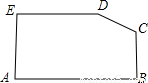
如图，已知五边形ABCDE中，∠ABC=∠AED=90°，AB=CD=AE=BC+DE=2，则五边形ABCDE的面积为________．
4
分析：可延长DE至F，使EF=BC，可得△ABC≌△AEF，连AC，AD，AF，可将五边形ABCDE的面积转化为两个△ADF的面积，进而求出结论．
解答：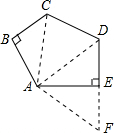
解：延长DE至F，使EF=BC，连AC，AD，AF，
∵AB=CD=AE=BC+DE，∠ABC=∠AED=90°，
由题中条件可得Rt△ABC≌Rt△AEF，△ACD≌△AFD，
∴SABCDE=2S△ADF=2×
•DF•AE=2××2×2=4．
故答案为：4．
点评：本题主要考查了全等三角形的判定及性质以及三角形面积的计算，注意对基础知识的熟练掌握及综合运用．
分析：可延长DE至F，使EF=BC，可得△ABC≌△AEF，连AC，AD，AF，可将五边形ABCDE的面积转化为两个△ADF的面积，进而求出结论．
解答：
解：延长DE至F，使EF=BC，连AC，AD，AF，∵AB=CD=AE=BC+DE，∠ABC=∠AED=90°，
由题中条件可得Rt△ABC≌Rt△AEF，△ACD≌△AFD，
∴SABCDE=2S△ADF=2×
•DF•AE=2××2×2=4．故答案为：4．
点评：本题主要考查了全等三角形的判定及性质以及三角形面积的计算，注意对基础知识的熟练掌握及综合运用．
练习册系列答案
阅读快车系列答案
相关题目
18、如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将五边形ABCDE分成面积相等的两部分的直线有
18、如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将该五边形ABCDE分成面积相等的两部分的直线有
如图，已知五边形ABCDE中，∠ABC=∠AED=90°，AB=CD=AE=BC+DE=2，则五边形ABCDE的面积为
如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将五边形ABCDE分成面积相等的两部分的直线有________条；满足条件的直线可以这样确定：________．