题目内容
如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将五边形ABCDE分成面积相等的两部分的直线有 条；满足条件的直线可以这样确定： ．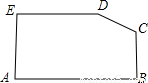
【答案】分析：题中所给的材料说明了平分该图面积的方法，其实质是根据梯形中位线定理矩形对角线的性质解答．
解答：
解：由题意得，可以将五边形ABCDE分成面积相等的两部分的直线有无数条．过梯形中位线中点以及矩形对角线的交点的直线即为所求．
设该直线与边CB、AE的交点分别为P、Q，线段PQ的中点为O，则经过点O且与边CB、AE相交的任意一条直线均可将该五边形的面积均分．
点评：此题考查学生对平行线分线段成比例定理及梯形中位线定理的理解及运用能力．
解答：
解：由题意得，可以将五边形ABCDE分成面积相等的两部分的直线有无数条．过梯形中位线中点以及矩形对角线的交点的直线即为所求．设该直线与边CB、AE的交点分别为P、Q，线段PQ的中点为O，则经过点O且与边CB、AE相交的任意一条直线均可将该五边形的面积均分．
点评：此题考查学生对平行线分线段成比例定理及梯形中位线定理的理解及运用能力．
练习册系列答案
金钥匙试卷系列答案
相关题目
18、如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将五边形ABCDE分成面积相等的两部分的直线有
18、如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将该五边形ABCDE分成面积相等的两部分的直线有
如图，已知五边形ABCDE中，∠ABC=∠AED=90°，AB=CD=AE=BC+DE=2，则五边形ABCDE的面积为
如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将五边形ABCDE分成面积相等的两部分的直线有________条；满足条件的直线可以这样确定：________．