题目内容
【题目】已知![]() 中,
中,![]() 过
过![]() 其中一个顶点的直线把
其中一个顶点的直线把![]() 分成两个等腰三角形.
分成两个等腰三角形.
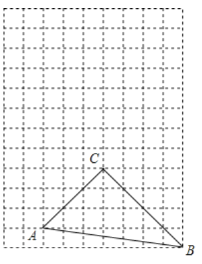
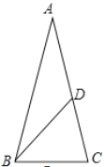
(1)如图1,若![]() 求
求![]() 的值;
的值;

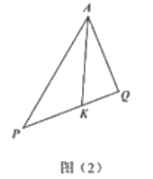
(2)![]() 度(
度(![]() 除外) ;
除外) ;
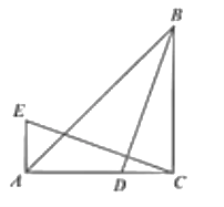
(3)如图2,![]() 为锐角,
为锐角,![]() 在
在![]() 延长线上,
延长线上,![]() 在边
在边![]() 上,
上,![]() 平分
平分![]() 交
交![]() 于
于![]() 请求线段
请求线段![]()
![]() 三者之者的数量关系. (用
三者之者的数量关系. (用![]() 表示)
表示)
【答案】(1)![]() ;(2)90
;(2)90![]() 或108
或108![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)如图,作底角![]() 的平分线BD,得到BD=AD,证得△ABC∽△BCD,得到
的平分线BD,得到BD=AD,证得△ABC∽△BCD,得到![]() ,通过计算即可求解;
,通过计算即可求解;
(2)利用三角形内角和定理并分类讨论求解;
(3)过Q作QH∥AP交AK的延长线于点H,作QG⊥AK于G,利用三角函数和等腰三角形的性质求得![]() ,
,![]() ,再利用相似三角形的性质得到
,再利用相似三角形的性质得到![]() ,即可求得线段
,即可求得线段![]()
![]() 三者之者的数量关系.
三者之者的数量关系.
(1)如图,作底角![]() 的平分线BD,
的平分线BD,
∵AB=AC,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BD=AD,
∴△ABC∽△BDC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
解得:![]() (负值已舍),
(负值已舍),
经检验,![]() 是原方程的解,
是原方程的解,
∴![]() ;
;
(2)①如图1,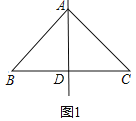
当过顶角的顶点的直线把它分成了两个等腰三角形,则AB=AC,AD=CD=BD,
设∠B=![]() ,
,
则∠BAD=∠B=![]() ,
,
∵AB=AC,
∴∠B=∠C=![]() ,
,
∴∠CAD=∠C=![]() ,
,
∵∠B+∠BAC+∠C=180°,
∴![]() ,
,
解得![]() ,
,
则![]() ;
;
②如图2,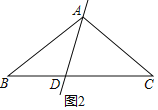
AB=AC=CD,BD=AD,
设∠C=![]() ,
,
∵AB=AC,
∴∠B=∠C=![]() ,
,
∵BD=AD,
∴∠BAD=∠B=![]() ,
,
∴∠ADC=∠B+∠BAD=2![]() ,
,
∵AC=CD,
∴∠CAD=∠ADC=2![]() ,
,
∴∠BAC=3![]() ,
,
∴![]() ,
,
![]() ,
,
则![]() ;
;
③如图3,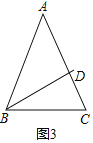
当过底角的角平分线把它分成了两个等腰三角形,则有AB=AC,BC=BD=AD,
设∠BAC=![]() ,
,
∵BD=AD,
∴∠ABD=∠BAC=![]() ,
,
∴∠CDB=∠ABD+∠BAC=2![]() ,
,
∵BC=BD,
∴∠C=∠CDB=2![]() ,
,
∵AB=AC,
∴∠ABC=∠C=2![]() ,
,
∵∠BAC+∠ABC+∠C=180°,
∴![]() +2
+2![]() +2
+2![]() =180°,
=180°,![]() =36°,
=36°,
则![]() =36°;
=36°;
④如图4,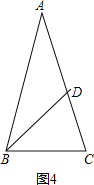
当∠BAC=![]() ,AD=BD,BC=DC,也符合,
,AD=BD,BC=DC,也符合,
∴∠BAC=∠ABD=![]() ,∠DBC=∠BDC=2
,∠DBC=∠BDC=2![]() ,
,
∵AB=AC,
∴∠ABC=∠ACB=3![]() ,
,
则![]() +3
+3![]() +3
+3![]() =180°,
=180°,
![]() ;
;
综上,除36![]() 外,
外,![]() 可以是90
可以是90![]() 或108
或108![]() 或
或![]() ;
;
故答案为:90![]() 或108
或108![]() 或
或![]() ;
;
(3)过Q作QH∥AP交AK的延长线于点H,作QG⊥AK于G,如图:
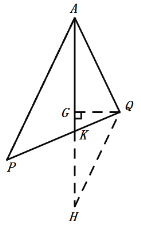
∵∠PAQ=![]() ,AK平分∠PAQ,
,AK平分∠PAQ,
∴∠PAH=∠QAH=![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵QH∥AP,
∴△HQK∽△APK,
∴![]() ,
,
∴![]() ,
,
∴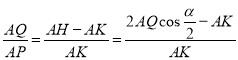 ,
,
故答案为:![]() .
.

 暑假作业安徽少年儿童出版社系列答案
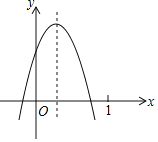
暑假作业安徽少年儿童出版社系列答案【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5