Question

【题目】如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述不正确的是( )

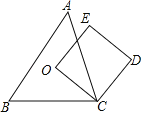
A.O是△AEB的外心，O不是△AED的外心

B.O是△BEC的外心，O不是△BCD的外心

C.O是△AEC的外心，O不是△BCD的外心

D.O是△ADB的外心，O不是△ADC的外心

Answer 1

【答案】C

【解析】

根据三角形的外心得出OA＝OC＝OA，根据正方形的性质得出OA＝OC＜OD，求出OA＝OB＝OC＝OE≠OD，再逐个判断即可

连接OB、OD、OA，

∵O为锐角三角形ABC的外心，

∴OA＝OC＝OA，

∵四边形OCDE为正方形，

∴OA＝OC＜OD，

∴OA＝OB＝OC＝OE≠OD，

∴OA＝OE≠OD，即O不是△AED的外心，

OA＝OE＝OB，即O是△AEB的外心，

OA＝OC＝OE，即O是△ACE的外心，

OB＝OA≠OD，即O不是△ABD的外心，

故选C．