题目内容
已知直线x=m(m>0)与双曲线y=
和直线y=-x-2分别相交于点A、B,且AB=7,求m的值.
| 6 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据题意求得A、B的坐标,然后根据AB=7列出关于m的方程,解方程即可求得m.
解答:解:∵直线x=m(m>0)与双曲线y=
和直线y=-x-2分别相交于点A、B,
∴点A、B的坐标分别为(m,
)、(m,-m-2),
∵AB=7,
∴
-(-m-2)=7,
整理得m2-5m+6=0,解得m1=2,m2=3.
经检验它们都是原方程的根,且符合题意,
所以m的值为2或3.
| 6 |
| x |
∴点A、B的坐标分别为(m,
| 6 |
| m |
∵AB=7,
∴
| 6 |
| m |
整理得m2-5m+6=0,解得m1=2,m2=3.
经检验它们都是原方程的根,且符合题意,
所以m的值为2或3.
点评:本题考查了反比例函数与一次函数的交点问题,交点坐标符合反比例函数的解析式,同时也符合一次函数的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列事件中的不可能事件是( )
| A、抛一枚硬币,落地后国徽一面朝下 |
| B、随意翻一下日历,翻到的号数是偶数 |
| C、这个月有雨 |
| D、今年夏天的最高气温达到了100℃ |
二次根式
,
,
,
,-
中,与
是同类二次根式的个数为( )
| 0.2 |
|
| 125 |
| 75 |
| 50 |
| 5 |
| A、2 | B、3 | C、4 | D、5 |
 已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=
已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=



 学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法,尝试用你积累的经验和方法解决下面问题.
学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法,尝试用你积累的经验和方法解决下面问题.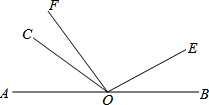 已知点O是直线AB上的一点,∠COE=120°,射线OF是∠AOE的一条三等分线,且∠AOF=
已知点O是直线AB上的一点,∠COE=120°,射线OF是∠AOE的一条三等分线,且∠AOF=