题目内容
2.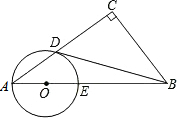 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD:AO=7:5,BC=3,求BD的长.
分析 (1)连接OD,由OA=OD得∠A=∠ODA,再由∠CBD+∠CDB=90°,∠A=∠CBD可得∠ODA+∠CDB=90°,即∠ODB=90°,于是根据切线的判定定理可判断BD为⊙O的切线;
(2)连结DE,如图,根据圆周角定理,由AE为直径得到∠ADE=90°,设AD=7t,AO=5t,AE=10t,得出AD:AE=7:10,接着证明△ADE∽△BCD得到,则利用比例性质得,得出BC:BD=AD:AE,可计算出BD.
解答 (1)证明:连接OD,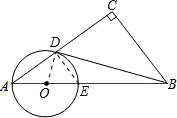
∵∠CBD=∠A,∠A=∠ADO,
∴∠CBD=∠ADO,
∵∠CBD+∠CDB=90°,
∴∠ADO+∠CDB=90°,
∴∠ODB=90°,
∴OD⊥BD,
∴BD与⊙O相切;
(2)解:∵AD:AO=7:5,
∴AD:AE=7:10,
∵AE为直径,
∴∠ADE=90°,
∵∠C=90°,
∴∠ADE=∠C,
∵∠CBD=∠ADO,
∴△ADE∽△BCD,
∴BC:BD=AD:AE,
∴BC:BD=7:10,
∵BC=3,
∴BD=$\frac{30}{7}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线;要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了解直角三角形和相似三角形的判定与性质.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
13.下列各组数据中,是勾股数的是( )
| A. | 0.3,0.4,0.5 | B. | $\frac{1}{6}$,$\frac{1}{8}$,$\frac{1}{10}$ | C. | 5,12,13 | D. | 8,12,15 |
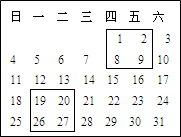 在日常生活中使用的日历表上,我们可以发现其中的某些数满足一定的规律,图中是2013年8月份的日历表.
在日常生活中使用的日历表上,我们可以发现其中的某些数满足一定的规律,图中是2013年8月份的日历表.