题目内容
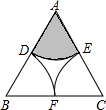 如图,有一边长为4的等边三角形纸片,要从中剪出三个面积相等的扇形,那么剪下的其中一个扇形
如图,有一边长为4的等边三角形纸片,要从中剪出三个面积相等的扇形,那么剪下的其中一个扇形ADE(阴影部分)的面积为
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
分析:扇形的面积公式是:S=
,代入公式就可以求出扇形的面积;根据圆锥的侧面积:S侧=
•2πr•l=πrl代入数据可得答案.
| nπr2 |
| 360 |
| 1 |
| 2 |
解答:解:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵要从中剪出三个面积相等的扇形,
∴AD=DB=
AB=2,
∴扇形ADE(阴影部分)的面积为:S=
=
π;
πrl=
π,
π×r×2=
π,
r=
,
故答案为:
π;
.
∴∠A=∠B=∠C=60°,
∵要从中剪出三个面积相等的扇形,
∴AD=DB=
| 1 |
| 2 |
∴扇形ADE(阴影部分)的面积为:S=
| nπR2 |
| 360 |
| 2 |
| 3 |
πrl=
| 2 |
| 3 |
π×r×2=
| 2 |
| 3 |
r=
| 1 |
| 3 |
故答案为:
| 2 |
| 3 |
| 1 |
| 3 |
点评:此题主要考查了扇形面积求法以及圆锥侧面展开图的性质,根据已知得出圆锥侧面展开图与圆锥各部分对应情况是解题关键.

练习册系列答案
相关题目
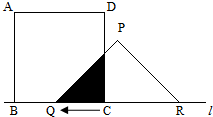 头所示方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:
头所示方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:
 如图,有一边长为8m的正方形大厅,它的地面是由形状、大小完全相同的黑白方砖密铺而成的,求一块方砖的边长.
如图,有一边长为8m的正方形大厅,它的地面是由形状、大小完全相同的黑白方砖密铺而成的,求一块方砖的边长.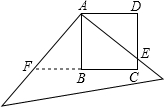 如图:有一边长为5cm的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在点A,两直角边与CD交于点E,与CB的延长线交于点F,则四边形AECF的面积为
如图:有一边长为5cm的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在点A,两直角边与CD交于点E,与CB的延长线交于点F,则四边形AECF的面积为