题目内容
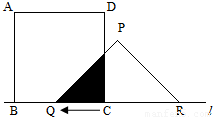
如图,有一边长为5cm的正方形ABCD和等腰△PQR,PQ=PR=5cm,QR=8cm,点B、C、Q、R在同一条直线l上,当C、Q两点重合时,等腰△PQR以1cm/秒的速度沿直线l按箭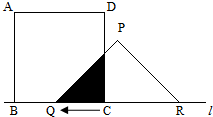 头所示方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:
头所示方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:(1)当t=3秒时,求S的值;
(2)当t=5秒时,求S的值;
(3)当5秒≤t≤8秒时,求S与t的函数关系式,并求出S的最大值.
分析:(1)当t=3时,CQ=3,过P作PE⊥QR于E,易求得PE的长和△QPE的面积,设PQ交CD于G,由于CG∥PE,可证得△CQG∽△EQP,根据相似三角形的面积比等于相似比的平方即可得到S的值.
(2)当t=5时,Q、B重合,线段PR与CD相交,设PR与CD相交于G,可仿照(1)的方法求得△RCG的面积,从而由△RPQ、△RCG的面积差求得阴影部分的面积.
(3)当5≤t≤8时,AB与PQ相交,RP与CD相交,仿照(1)的方法,可求得正方形外部的两个小三角形的面积,进而可参照(2)的方法求得阴影部分的面积表达式,由此可得到关于S、t的函数关系式,根据函数的性质即可得到S的最大值.
(2)当t=5时,Q、B重合,线段PR与CD相交,设PR与CD相交于G,可仿照(1)的方法求得△RCG的面积,从而由△RPQ、△RCG的面积差求得阴影部分的面积.
(3)当5≤t≤8时,AB与PQ相交,RP与CD相交,仿照(1)的方法,可求得正方形外部的两个小三角形的面积,进而可参照(2)的方法求得阴影部分的面积表达式,由此可得到关于S、t的函数关系式,根据函数的性质即可得到S的最大值.
解答: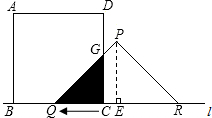 解:(1)作PE⊥QR,E为垂足.
解:(1)作PE⊥QR,E为垂足.
∵PQ=PR,
∴QE=RE=
QR=4,
在Rt△PEQ中
∴PE=
=3;(1分)
当t=3时,QC=3,设PQ与DC交于点G.
∵PE∥DC,
∴△QCG∽△QEP.(2分)
∴
=(
)2,
∵S△QEP=
×4×3=6,
∴S=(
)2×6=
(cm2).(3分)
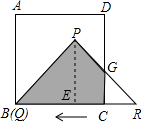
(2)当t=5时,CR=3.
设PR与DC交于G,由△RCG∽△REP,可求出CG=
,
所以,S△RCG=
×3×
=
(cm2),(5分)
S=12-
=
(cm2).(6分)
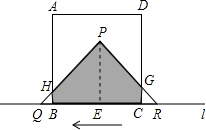 (3)当5≤t≤8时,QB=t-5,RC=8-t,设PQ交AB于点H,
(3)当5≤t≤8时,QB=t-5,RC=8-t,设PQ交AB于点H,
由△QBH∽△QEP,EQ=4,∴BQ:EQ=(t-5):4,
∴S△BQH:S△PEQ=(t-5)2:42,又S△PEQ=6,
∴S△QBH=
(t-5)2(7分)
由△RCG∽△REP,同理得S△RCG=
(8-t)2(8分)
∴S=12-
(t-5)2-
(8-t)2.即S=-
t2+
t-
(9分)
当t=-
=
时,S最大,S的最大值=
=
(cm2).(10分)
 解:(1)作PE⊥QR,E为垂足.
解:(1)作PE⊥QR,E为垂足.∵PQ=PR,
∴QE=RE=
| 1 |
| 2 |
在Rt△PEQ中
∴PE=
| 52-42 |
当t=3时,QC=3,设PQ与DC交于点G.
∵PE∥DC,
∴△QCG∽△QEP.(2分)
∴
| S |
| S△QEP |
| 3 |
| 4 |
∵S△QEP=
| 1 |
| 2 |
∴S=(
| 3 |
| 4 |
| 27 |
| 8 |

(2)当t=5时,CR=3.
设PR与DC交于G,由△RCG∽△REP,可求出CG=
| 9 |
| 4 |
所以,S△RCG=
| 1 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
S=12-
| 27 |
| 8 |
| 69 |
| 8 |
 (3)当5≤t≤8时,QB=t-5,RC=8-t,设PQ交AB于点H,
(3)当5≤t≤8时,QB=t-5,RC=8-t,设PQ交AB于点H,由△QBH∽△QEP,EQ=4,∴BQ:EQ=(t-5):4,
∴S△BQH:S△PEQ=(t-5)2:42,又S△PEQ=6,
∴S△QBH=
| 3 |
| 8 |
由△RCG∽△REP,同理得S△RCG=
| 3 |
| 8 |
∴S=12-
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 39 |
| 4 |
| 171 |
| 8 |
当t=-
| ||
2×(-
|
| 13 |
| 2 |
| 4ac-b2 |
| 4a |
| 165 |
| 16 |
点评:此题考查了正方形的性质、等腰三角形的性质、相似三角形的判定和性质、图形面积的求法等知识,熟练掌握相似三角形的性质(相似三角形的面积比等于相似比的平方)是解答此题的关键.

练习册系列答案
相关题目
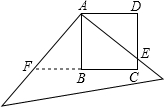 如图:有一边长为5cm的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在点A,两直角边与CD交于点E,与CB的延长线交于点F,则四边形AECF的面积为
如图:有一边长为5cm的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在点A,两直角边与CD交于点E,与CB的延长线交于点F,则四边形AECF的面积为