题目内容
6. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是$\widehat{CAD}$上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系,并说明理由.
(2)点P′在劣弧$\widehat{CD}$上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.
分析 (1)连接OD,根据圆周角定理得到∠CPD=$\frac{1}{2}$∠COD,根据垂径定理得到$\widehat{BC}$=$\widehat{BD}$,得到∠BOC=∠BOD,等量代换即可;
(2)根据圆内接四边形的性质解答即可.
解答 解:(1)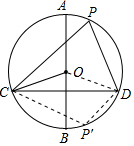 ∠CPD=∠COB.
∠CPD=∠COB.
理由如下:连接OD,
由圆周角定理得,∠CPD=$\frac{1}{2}$∠COD,
∵AB是直径,CD是弦,AB⊥CD,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠BOC=∠BOD=$\frac{1}{2}$∠COD,
∴∠CPD=∠COB.
(2)∵四边形PCP′D是圆内接四边形,
∴∠CP′D+∠CPD=180°,
∴∠CP′D+∠COB=180°.
点评 本题考查的是垂径定理、圆周角定理和圆内接四边形的性质的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.

练习册系列答案
相关题目
 如图:梯形ABCD,AD∥BC,对角线AC、BD交于点E,AD=2,BC=3,S△AED=2,则S梯形ABCD=12.5.
如图:梯形ABCD,AD∥BC,对角线AC、BD交于点E,AD=2,BC=3,S△AED=2,则S梯形ABCD=12.5.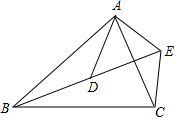 如图,在△ABC中,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.求证:∠BAD=∠CAE.
如图,在△ABC中,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.求证:∠BAD=∠CAE. 如图,已知:△ABC和直线l,请作出△ABC关于直线l的对称三角形.
如图,已知:△ABC和直线l,请作出△ABC关于直线l的对称三角形.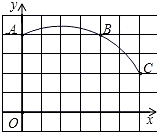 如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),C点坐标为(6,2),D点坐标为(7,0),求证:直线CD是圆的切线.
如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),C点坐标为(6,2),D点坐标为(7,0),求证:直线CD是圆的切线.