��Ŀ����
����Ŀ��ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г�����������
�������飬�õ��������ݣ�
���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | 100 | �� |
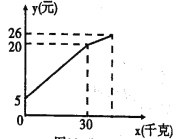
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵʽ�������������ϵʽ��
��2����۲��Ź涨���ù���Ʒ�����۵�����߲�����45Ԫ/���������۵���x��Ϊ����ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��������=�����ܼ۩��ɱ��ܼۣ�
��3�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�

���𰸡���1��y=��10x+700����2�������۵���x��Ϊ30Ԫʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ����3����x=40ʱ��W�����ֵ9000
�������������������1��������㷨�ó�����λ�ã��������ô���ϵ������һ�κ�������ʽ���ɣ�
��2����������=�����ܼ�-�ɱ��ܼۻ�����������������=���������ó���ʽ������ɣ�
��3��������������������=��������W=��x-10����-10x+700�������ֵ���ɣ�
�����������1����ͼ����ͼ��

��ͼ�ɲ��룬y��x��һ�κ�����ϵ�������һ�κ���Ϊy=kx+b��k��0����
�����һ�κ�����ͼ����㣨20��500������30��400��
��![]() ��
��
��ã� ![]() ��
��
��һ�κ����Ĺ�ϵʽ�ǣ�y=-10x+700��
��2��������ɵã���x-10����-10x+700��=8000��
��ã�x=30��x=50������������ȥ��
�ʵ����۵���x��Ϊ30Ԫʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��
��3���蹤�ճ������ù���Ʒÿ���õ�������WԪ��������ã�
W=��x-10����-10x+700��
=-10x2+800x-7000
=-10��x-40��2+9000
�ʵ�x=40ʱ��W�����ֵ9000��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�����о��С���ʮ�߽���Сѧ���鷨��������Ʒ��������֪ÿ��������Ʒ�ɼ���Ϊ![]() ����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
������ | Ƶ�� | �ٷֱ� |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
�ϼ� | ________ | 1 |

����������Ϣ������������⣺
��1������鷨��Ʒ�����ɼ��ĵ����Dz���_____����ղ顱�������顱����������_____��
��2������ϱ�������ȫ�鷨��Ʒ�����ɼ�Ƶ��ֱ��ͼ��
��3����80�֣���80�֣����ϵ��鷨��Ʒ������Ϊ�ȼ������Թ���ȫ�л�õȼ�����������