题目内容
11.反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-1,-2),且自变量x>1时,函数值y的取值范围是( )| A. | 0<y<2 | B. | y>2 | C. | y<1 | D. | y>1 |
分析 先把点(-1,-2)代入y=$\frac{k}{x}$可求出k,确定反比例函数的解析式为y=$\frac{2}{x}$,根据反比例函数的性质得图象分布在第一、三象限,在每一象限,y随x的增大而减小,而x=1时,y=2,所以当x>1时,0<y<2.
解答 解:∵反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-1,-2),
∴k=-1×(-2)=2,
∴反比例函数的解析式为y=$\frac{2}{x}$,
∴图象分布在第一、三象限,在每一象限,y随x的增大而减小,
当x=1时,y=2,
∴0<y<2,
故选:A.
点评 本题考查了反比例函数图象上点的坐标特征以及反比例函数的性质,关键是掌握反比例函数图象上的点的坐标满足其解析式.

练习册系列答案
相关题目
1.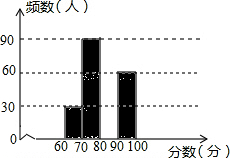 某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:
某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:
根据以上图表信息,解答下列问题:
(1)补全频数分布表和频数直方图;
(2)参赛的小明同学认为他的比赛成绩是所有参赛同学成绩的中位数,据此推断他的成绩落在80≤x<90分数段内;
(3)如果该校共有2000名学生参赛,比赛成绩80分以上(含80分)为“优秀”,请估计该校获得“优秀”等级的人数.
 某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:
某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | |
| 80≤x<90 | 0.4 | |
| 90≤x<100 | 60 | 0.2 |
(1)补全频数分布表和频数直方图;
(2)参赛的小明同学认为他的比赛成绩是所有参赛同学成绩的中位数,据此推断他的成绩落在80≤x<90分数段内;
(3)如果该校共有2000名学生参赛,比赛成绩80分以上(含80分)为“优秀”,请估计该校获得“优秀”等级的人数.
2.下列图形中,中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.在比例尺为1:10000 000的地图上,量得甲、乙两地的距离是3cm,则两地的实际距离是( )
| A. | 3×105m | B. | 3.3×105m | C. | 3×106m | D. | 3.3×106m |
16.2sin30°-tan45°的值等于( )
| A. | $\sqrt{3}-1$ | B. | $\sqrt{2}-1$ | C. | 0 | D. | $-\frac{1}{2}$ |
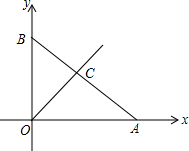 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+3$的图象分别交x轴,y轴交于A,B两点,与一次函数y=x的图象交于第一象限内的点C.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+3$的图象分别交x轴,y轴交于A,B两点,与一次函数y=x的图象交于第一象限内的点C.