题目内容
在△ABC中,sinB=cos(90°-C)= ,那么△ABC是
,那么△ABC是
- A.等腰三角形
- B.等边三角形
- C.直角三角形
- D.等腰直角三角形
A
分析:由题意可证∠C=∠B=30°,即证△ABC是等腰三角形.
解答:sinB=cos(90°-C)= ,
,
即sinB= ,∴∠B=30°;
,∴∠B=30°;
cos(90°-C)= ,
,
∴90°-∠C=60°,
∴∠C=30°,
∴∠C=∠B.
∴△ABC是等腰三角形.
故选A.
点评:熟记特殊角的三角函数值是解题的关键,还考查了等腰三角形的判断.
分析:由题意可证∠C=∠B=30°,即证△ABC是等腰三角形.
解答:sinB=cos(90°-C)=
 ,
,即sinB=
 ,∴∠B=30°;
,∴∠B=30°;cos(90°-C)=
 ,
,∴90°-∠C=60°,
∴∠C=30°,
∴∠C=∠B.
∴△ABC是等腰三角形.
故选A.
点评:熟记特殊角的三角函数值是解题的关键,还考查了等腰三角形的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,sin∠B=
如图,在△ABC中,sin∠B=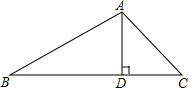 如图,在△ABC中,sin∠B=
如图,在△ABC中,sin∠B= 如图,在△ABC中,sin∠B=
如图,在△ABC中,sin∠B= ,∠C=30°,AB=10.
,∠C=30°,AB=10. 如图,在△ABC中,sin∠B=
如图,在△ABC中,sin∠B=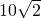 ,求线段BD的长.(结果保留根号)
,求线段BD的长.(结果保留根号) ,∠C=30°,AB=10.
,∠C=30°,AB=10.