题目内容
如图，在等腰梯形ABCD中，AD∥BC．O是CD边的中点，以O为圆心，OC长为半径作圆，交BC边于点E．过E作EH⊥AB，垂足为H．已知⊙O与AB边相切，切点为F
(1)求证：OE∥AB；
(2)求证：EH=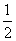
AB；
(3)若AD与⊙O也相切，如图二，已知BE(BC)=5，BH=3，求⊙O的半径
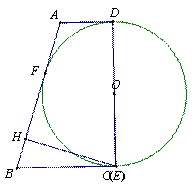
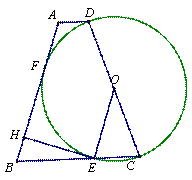
图一 图二
（1）∵ABCD是等腰梯形 ∴∠B=∠C （1分）
∵OE=OC ∴∠OEC=∠C （1分）
∴∠OEC=∠B ∴OE∥AB （1分）
（2）连结OF
∵AB与⊙O相切与点F ∴∠OFB=90°（1分）
又∵EH⊥AB ，OE∥AB
∴∠OEH=∠EHF=90°
∴四边形OFHE是矩形 （1分）
∵OE=OF
∴四边形OFHE是正方形 （1分）
∴EH=OE=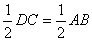
（1分）
（3）连结OF、OB
∵AD与圆相切
∴∠ADC=90°
∵AD∥BC
∴∠DCB=90°
∵∠OFB=∠OCB=90°,OF=OC ,OB=OB
∴⊿OFB≌⊿OBC
∴BF=BC=5 （1分）
∵BH=3
∴HF=2 ,HC=4
过点O作OM⊥CH与点M，在⊿OMC中设OC=r
可得r2-(4-r)2=22 （1分）
∴r=2.5 （1分） ∴⊙O半径是2.5
练习册系列答案
相关题目
，求分式
的值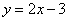
上，且点A到两坐标轴的距离相等，则点A在第一或第四象限．（3）半径为5的圆中，弦AB＝8，则圆周上到直线AB的距离为2的点共有四个．（4）若A（
，
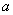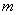）、B（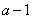
，
）(
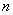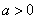)在反比例函数
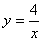的图象上，则
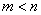．（5）用反证法证明命题“在一个三角形中，至少有一个内角不小于
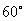”，可先假设三角形中每一个内角都小于
=
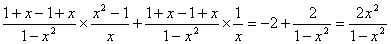
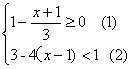由（1）得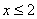
； 由（2）得
∴ 
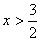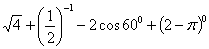=2+2-1+1=4
