题目内容
4．一列快车从甲站开往乙站，每小时行xkm，同时，一列慢车从乙站开往甲站，每小时行ykm，t小时后两辆车相遇，则走完全程慢车比快车多用了多少小时？先列代数式，再计算当x=72，y=56，t=7$\frac{7}{8}$时，代数式的值．分析 首先求得甲站到乙站的路程为（x+y）tkm，再分别表示出用快车行完路程用的时间，慢车行完路程用的时间，进一步相减即可；最后代入字母数值求得答案即可．
解答 解：走完全程慢车比快车多用了$\frac{（x+y）t}{y}$-$\frac{（x+y）t}{x}$小时；
当x=72，y=56，t=7$\frac{7}{8}$时，
原式=$\frac{（72+56）×\frac{63}{8}}{56}$-$\frac{（72+56）×\frac{63}{8}}{72}$=18-14=4．
点评 此题考查列代数式以及代数式求值，掌握行程问题中的基本数量关系是解决问题的关键．
练习册系列答案
相关题目
9．若（x-2z）2+|2x-1|+|y+3|=0，则满足等式的x、y、z分别是（ ）
| A． | x=$\frac{1}{2}$，y=3，z=1 | B． | x=-$\frac{1}{2}$，y=-3，z=-1 | C． | x=$\frac{1}{2}$，y=-3，z=$\frac{1}{4}$ | D． | x=$\frac{1}{2}$，y=3，z=2 |
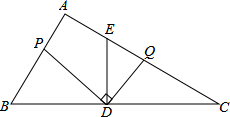如图，在Rt△ABC中，∠A=90°，AB=12，AC=16，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上的一动点，点Q为边AC上的一动点，且∠PDQ=90°．