题目内容
已知a2-4a+b2-
+
=0,则a2-4
= .
| b |
| 2 |
| 65 |
| 16 |
| b |
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:首先分组分解因式,进一步利用非负数的性质求得a、b,代入求得数值即可.
解答:解:∵a2-4a+b2-
+
=0,
a2-4a+4+b2-
+
=0,
(a-2)2+(b-
)2=0,
∴a-2=0,b-
=0,
∴a=2,b=
,
∴a2-4
=22-4
=4-2=2.
故答案为:2.
| b |
| 2 |
| 65 |
| 16 |
a2-4a+4+b2-
| b |
| 2 |
| 1 |
| 16 |
(a-2)2+(b-
| 1 |
| 4 |
∴a-2=0,b-
| 1 |
| 4 |
∴a=2,b=
| 1 |
| 4 |
∴a2-4
| b |
|
故答案为:2.
点评:此题考查配方法的运用,以及非负数的性质,注意式子特点,灵活运用完全平方公式解决问题.

练习册系列答案
相关题目
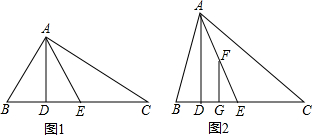
 在△ABC中,∠ACB=70°,∠BAC=65°,AD⊥BC于点D,BE⊥AC于E,AD与BE交于H,则∠CHD=
在△ABC中,∠ACB=70°,∠BAC=65°,AD⊥BC于点D,BE⊥AC于E,AD与BE交于H,则∠CHD=