Question

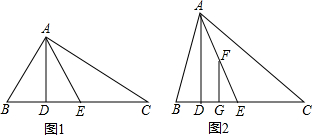
如图1所示，△ABC中，AD⊥BC，AE平分∠BAC．
（1）若∠B=70°，∠C=30°，求∠DAE的度数；
（2）△ABC中，若∠B=α，∠C=β（α＞β），请你根据（1）问的结果大胆猜想∠DAE与α，β间的等量关系，并说明理由；
（3）如图2所示，F是AE上任意一点过F作FG垂直BC于G，若∠B=80°，∠C=40°，运用（2）的结论求出∠EFG的度数．

Answer 1

考点：三角形内角和定理,三角形的外角性质

专题：

分析：（1）求出∠BAC度数，求出∠CAE度数，求出∠CAD，相减即可．
（2）求出∠BAC度数，求出∠CAE度数，求出∠CAD，相减即可．
（3）推出AD∥FG，根据平行线性质得出∠EFG=∠DAE，代入即可．

解答：解：（1）∵∠B=70°，∠C=30°，
∴∠BAC=180°-（∠B+∠C）=180°-30°-70°=80°，
∵AE平分∠BAC，
∴∠BAE=

1

2

∠BAC=

1

2

×80°=40°，
∵AD⊥BC，
∴∠ADB=90°，
∵∠B=70°，
∴∠DAB=180°-90°-70°=20°，
∴∠DAE=∠BAE-∠BAD=40°-20°=20°；

（2）∠DAE=

1

2

α-

1

2

β，
理由是：∵∠C=β，∠B=α，
∴∠BAC=180°-（∠B+∠C）=180°-α-β，
∵AE平分∠BAC，
∴∠CAE=

1

2

∠BAC=

1

2

×（180°-α-β）=90°-

1

2

α-

1

2

β，
∵AD⊥BC，
∴∠ADC=90°，
∵∠C=β，
∴∠DAB=180°-90°-α=90°-α，
∴∠DAE=∠BAE-∠BAD=90°-

1

2

α-

1

2

β-（90°-α）=

1

2

α-

1

2

β；

（3）∵∠C=40°，∠B=80°，
∴∠DAE=

1

2

×80°-

1

2

×40°=20°，
∵AD⊥BC，FG⊥BC，
∴∠ADE=∠FGE=90°，
∴AD∥FG，
∴∠EFG=∠DAE=20°．

点评：本题考查了垂直定义，三角形内角和定理，角平分线定义，平行线的性质和判定的应用．