题目内容
14.若x2-3x+1=0,求$\frac{{x}^{3}+\frac{1}{{x}^{3}}+7}{{x}^{4}+\frac{1}{{x}^{4}}+3}$的值.分析 根据题目中的式子变形可以求得x+$\frac{1}{x}$的值,然后将所求式子变形即可解答本题.
解答 解:∵x2-3x+1=0,
∴x-3+$\frac{1}{x}=0$,
∴x+$\frac{1}{x}$=3,
∴$\frac{{x}^{3}+\frac{1}{{x}^{3}}+7}{{x}^{4}+\frac{1}{{x}^{4}}+3}$
=$\frac{(x+\frac{1}{x})({x}^{2}-1+\frac{1}{{x}^{2}})+7}{({x}^{2}+\frac{1}{{x}^{2}})^{2}+1}$
=$\frac{(x+\frac{1}{x})[(x+\frac{1}{x})^{2}-3]+7}{[(x+\frac{1}{x})^{2}-2]^{2}+1}$
=$\frac{3×({3}^{2}-3)+7}{({3}^{2}-2)^{2}+1}$
=$\frac{25}{50}$
=$\frac{1}{2}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
2.若-3x2ny3与2x4ym是同类项,则|m-n|( )
| A. | -1 | B. | 7 | C. | 1 | D. | 0 |

 请写出图中所有的邻补角,同位角及内错角.
请写出图中所有的邻补角,同位角及内错角.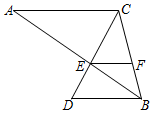 如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.
如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.