题目内容
小红、小明、小颖三人对代数式x2-4x-5进行探究后,得到了两个不同的结论.
小红:①代数式x2-4x-5有最小值是-9.
小明:②抛物线y=x2-4x-5与x轴的交点为(5,0),(-1,0).
(1)请你判断他们的结论的正确的有 .
(2)选择其中一个正确的结论加以证明.
小红:①代数式x2-4x-5有最小值是-9.
小明:②抛物线y=x2-4x-5与x轴的交点为(5,0),(-1,0).
(1)请你判断他们的结论的正确的有
(2)选择其中一个正确的结论加以证明.
考点:抛物线与x轴的交点,配方法的应用
专题:
分析:①先把代数式x2-4x-5通过配方变形为(x-2)2-9的形式,再根据(x-2)2≥0,即可得出答案.
②当y=0时求出抛物线与x轴的交点坐标.
②当y=0时求出抛物线与x轴的交点坐标.
解答:解:(1)正确的结论有:①②.
(2)选择①.理由如下:
∵x2-4x-5=x2-4x+4-4-5=(x-2)2-9,
∵(x-2)2≥0,
∴(x-2)2-9≥-9,
∴当x=2时,代数式x2-4x-5有最小值是-9.
选择②.理由如下:
当y=0时,有x2-4x-5=0,即(x-5)(x+1)=0,
解得:x1=5,x2=-1,
故抛物线与x轴的交点坐标为(5,0),(-1,0).
(2)选择①.理由如下:
∵x2-4x-5=x2-4x+4-4-5=(x-2)2-9,
∵(x-2)2≥0,
∴(x-2)2-9≥-9,
∴当x=2时,代数式x2-4x-5有最小值是-9.
选择②.理由如下:
当y=0时,有x2-4x-5=0,即(x-5)(x+1)=0,
解得:x1=5,x2=-1,
故抛物线与x轴的交点坐标为(5,0),(-1,0).
点评:此题考查了抛物线与x轴的交点,配方法的应用,关键是通过配方把原来的代数式转化成a(x-h)2+k的形式,要掌握配方法的步骤.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
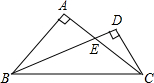 如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD.
如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD. 如图,一只密封的长方体盒子,长、宽、高分别是5cm、4cm、3cm.现在一只蚂蚁由A点出发去G点觅食,求这只蚂蚁从A点爬行到G的最短路短是路程.
如图,一只密封的长方体盒子,长、宽、高分别是5cm、4cm、3cm.现在一只蚂蚁由A点出发去G点觅食,求这只蚂蚁从A点爬行到G的最短路短是路程. 如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC、∠BCD,求证:AE=ED.
如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC、∠BCD,求证:AE=ED.