题目内容
5. 如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.
如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.(1)求证:AM=CN;
(2)联结BD,如果BD是AC与MN的比例中项,求证:BE⊥AD.
分析 (1)根据菱形的四条边都相等可得AB=BC,对角相等可得∠BAM=∠BCN,对角线平分一组对角线可得∠BAM=∠DAM=∠DCA=∠BCA,然后利用“SAS”证明△ABE和△CBF全等,然后利用全等三角形对应边相等证明即可.
(2)只要证明△BOM∽△AOB,得∠OBM=∠BAO=∠DAC,再根据∠OBM+∠BMO=90°,∠AME=∠OMB,即可证明.
解答 (1)证明:如图1中,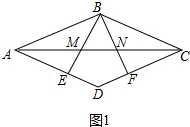
∵四边形ABCD为菱形,
∴AB=BC,∠BAM=∠BCN,∠BAM=∠DAM=∠DCA=∠BCA,
在△ABE和△CBF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠BCF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CBF(ASA),
∴AE=CF.
(2)如图2中,连接BD交AC于O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠BAC=∠DAC,
∵AM=CN(由(1)可知),
∴OM=ON,
∴BD=2OB,AC=2AO,MN=2OM,
∵BD2=MN•AC,
∴4•OB2=2OM•2OA,
∴OB2=OM•OA,
∴$\frac{OB}{OM}$=$\frac{OA}{OB}$,∵∠BOM=∠AOB=90°,
∴△BOM∽△AOB,
∴∠OBM=∠BAO=∠DAC,
∵∠OBM+∠BMO=90°,∠AME=∠OMB,
∴∠EAM+∠AME=90°,
∴∠AEM=90°,即BE⊥AD.
点评 本题考查了菱形的性质,全等三角形的判定与性质,相似三角形的判定和性质,等角的余角相等的性质比例中项等知识,熟记各性质并确定出全等三角形是解题的关键,第二个问题的关键是正确寻找相似三角形解决问题,属于中考常考题型.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.已知x为实数,且$\frac{3}{{x}^{2}+9x}-({x}^{2}+9x)=2$,那么x2+9x的值为( )
| A. | 1 | B. | -3或1 | C. | 3 | D. | -1或3 |
13. 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2013 | B. | ($\frac{\sqrt{2}}{2}$)2014 | C. | ($\frac{1}{2}$)2013 | D. | ($\frac{1}{2}$)2014 |
20.一个等腰三角形的两条边长分别是方程x2-7x+10=0的两根,则这个等腰三角形的腰长是( )
| A. | 2 | B. | 5 | C. | 2或5 | D. | 3或4 |
10.平行四边形的一边长是6,则它的对角线长可能是( )
| A. | 4和8 | B. | 2和12 | C. | 4和6 | D. | 2和14 |
 如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点. 如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )