Question

如图a，P为△ABC内任一点，试证明∠BPC=∠ABP＋∠ACP＋∠A．

　　　　　　  

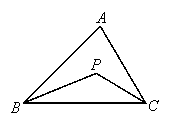
变式一　如图，若点P为△ABC两角∠ABC和∠ACB的平分线的交点，则∠BPC和∠A有怎样的关系?

变式二　如图，“变式一”已知不动，另补上“若点Q是它们外角平分线的交点”，则∠BPC和∠Q有何关系?

变式三　一个零件的形状如图所示，按规定∠A应等于90°，∠B、∠C分别是21°和32°．检验工人量得∠BDC=148°．就断定这个零件不合格，这是为什么?

Answer 1

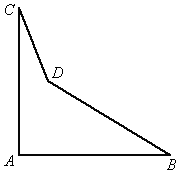
答案：略
解析：

证明 　 如上图b，延长BP交AC于点D． ∵∠PDC是△ABD的一个外角， ∴∠PDC=∠A＋∠ABP． 同理　∠BPC=∠PDC＋∠ACP． ∴∠BPC=∠ABP＋∠ACP＋∠A． 变式一 解 　 由已知，得∠1=∠ABC，∠2=∠ACB． 在△BPC中，∠1＋∠2＋∠BPC=180°． ∴∠BPC=180°－(∠ABC＋∠ACB)． 在△ABC中，∠ABC＋∠ACB＋∠A=180°． ∴ 　　　　 变式二 解 　 由“变式一”可知：∠BPC=90°＋∠A， 易知：∠Q=90°－∠A，故∠BPC＋∠Q= ∠BPC＋∠Q=180° 变式三 解 　 连接BC，点D是△ABC内任一点，则∠BDC=∠ABD＋∠ACD＋∠A，本题就是因为，故判定这个零件不合格．

提示：

∠BPC与∠ABP、∠ACP、∠A这三个角既不在同一个三角形中，又不存在对顶角、邻补角、外角等关系，已知条件很简单、难以直接得出别的结论，所以应考虑作辅助线，使这些角发生联系． 由图形中四个角的位置特点和所说明等式特点想到“三角形一个外角等于与它不相邻的两个内角和”的性质，故延长BP交AC于点D，于是有∠BPC=∠ACP＋∠PDC，又∠PDC=∠A＋∠ABP．从而问题得以解决． 由已知条件和所求部分，应想到∠BPC与∠1、∠2的关系：∠BPC=180°－(∠1＋∠2)． 而∠1=∠ABC，∠2=∠ACB． 到此应想到∠ABC、∠ACB与∠A的关系：∠ABC＋∠ACB＋∠A=180°．