题目内容
如图，点G为△ABC重心，DE经过点G，DE∥BC，CEF∥AB，S△ABC=18，求四边形BDEF面积．分析：由于点G为△ABC重心，利用重心的性质等等等
=
，而由△ADE∽△ABC得到
=(
)2，然后利用已知条件可以求出S△ADE=8，和S△CEF，最后根据图形可以求出四边形BDEF的面积．
| AD |
| AB |
| 2 |
| 3 |
| S△ADE |
| S△ABC |
| 2 |
| 3 |
解答：解：∵点G为△ABC重心，DE经过点G，DE∥BC，
∴
=
，
∵△ADE∽△ABC，
∴
=(
)2，
∵S△ABC=18，∴S△ADE=8，
同理可得 S△CEF=2，
∴四边形BDEF的面积等于18-8-2=8．
∴
| AD |
| AB |
| 2 |
| 3 |
∵△ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| 2 |
| 3 |
∵S△ABC=18，∴S△ADE=8，
同理可得 S△CEF=2，
∴四边形BDEF的面积等于18-8-2=8．
点评：此题分别考查了相似三角形的判定与性质、重心的性质及平行线的性质，解题时首先利用重心的性质，然后利用相似三角形的判定与性质即可解决问题．
练习册系列答案
阅读快车系列答案
相关题目
12、如图，点H为△ABC的垂心，以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D，延长AD交CH于点P，
25、尺规作图（不写作法，但要保留作图痕迹）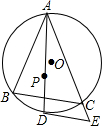
如图，点P为△ABC的内心，延长AP交△ABC的外接圆⊙O于D，过D作DE∥BC，交AC的延长线于E点．①则直线DE与⊙O的位置关系是
如图，点G为△ABC的重心，DE过点G，且DE∥BC，EF∥AB，那么CF：BF=
如图，点E为△ABC边AB上一点，AC=BC=BE，AE=EC，BD⊥AC于D，求∠CBD的度数．