题目内容
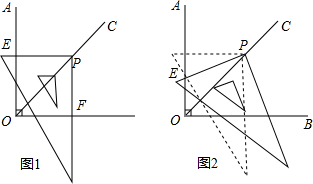
已知：如图，AB=AD，∠ABC=∠ADC．试说明：CB=CD．考点：等腰三角形的判定与性质
专题：证明题
分析：连接BD，由AB=AD，根据等边对等角，可得∠ADB=∠ABD，由∠ABC=∠ADC，根据等式的基本性质，可得∠CBD=∠CDB，根据等角对等边，所以CD=CB．
解答：证明：连接BD，
∵AB=AD，
∴∠ADB=∠ABD，
∵∠ABC=∠ADC，
∴∠ABC-∠ABD=∠ADC-∠ADB，
即∠CBD=∠CDB，
∴CD=CB．
∵AB=AD，
∴∠ADB=∠ABD，
∵∠ABC=∠ADC，
∴∠ABC-∠ABD=∠ADC-∠ADB，
即∠CBD=∠CDB，
∴CD=CB．
点评：此题考查了等腰三角形的判定与性质，用角相等来求边相等是本题的解题思路．
练习册系列答案
初中暑期衔接系列答案
相关题目
