题目内容
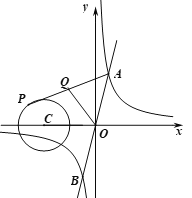
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .
.
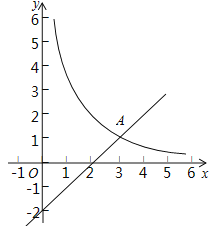
(1)求k、m的值;
(2)已知点![]() ,过点P作平行于x轴的直线,交直线
,过点P作平行于x轴的直线,交直线![]() 于点M,过点P作平行于y轴的直线,交函数
于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当![]() 时,判断线段PM与PN的数量关系,并说明理由;
时,判断线段PM与PN的数量关系,并说明理由;
②用含n的式子表示PN,则![]() ________.
________.
③若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.
【答案】(1)m=1,k=3;(2)①![]() ,理由见解析,②
,理由见解析,②![]() ,③
,③![]() 或
或![]() .
.
【解析】
(1)将A点代入![]() 中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值;
中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值;
(2)①当![]() 时,分别求出M、N两点的坐标即可求出PM与PN的关系;
时,分别求出M、N两点的坐标即可求出PM与PN的关系;
②由PN∥y轴,可用含n的代数式表示出点N的坐标,然后利用两点间的距离公式即可得出答案;
③由题意可求得点M的坐标,进而可得PM的长,由![]() ,再根据图象即可求出n的范围.
,再根据图象即可求出n的范围.
解:(1)将![]() 代入
代入![]() ,
,![]() ,
,![]() ,
,
将![]() 代入
代入![]() ,
,![]() ;
;
(2)①当![]() 时,
时,![]() ,如图,
,如图,
令![]() ,代入
,代入![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
令![]() ,代入
,代入![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
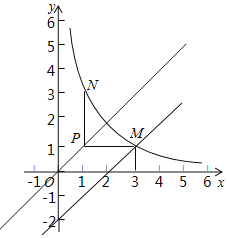
②∵![]() ,N(n,
,N(n,![]() ),∴PN=
),∴PN=![]() .
.
故答案为:![]() ;
;
③∵![]() ,∴点P在直线
,∴点P在直线![]() 上,
上,
过点P作平行于x轴的直线,交直线![]() 于点M,则
于点M,则![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() ≥2,结合图象可得:
≥2,结合图象可得:![]() 或
或![]() .
.

练习册系列答案
相关题目