题目内容
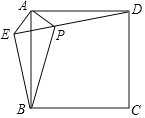
【题目】定义：角的内部一点到角两边的距离比为1：2，这个点与角的顶点所连线段称为这个角的二分线．如图1，点P为∠AOB内一点，PA⊥OA于点A，PB⊥OB于点B，且PB＝2PA，则线段OP是∠AOB的二分线．
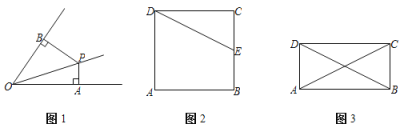
（1）图1中，OP为∠AOB的二分线，PB＝4，PA＝2，且OA+OB＝8，求OP的长；
（2）如图2，正方形ABCD中，AB＝2，点E是BC中点，证明：DE是∠ADC的二分线；
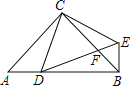
（3）如图3，四边形ABCD中，AB∥CD，∠ABC＝90°，且∠CAB＜∠CAD，∠BDC＜∠BDA，若AC，BD分别是∠DAB，∠ADC的二分线，证明：四边形ABCD是矩形．
【答案】（1）OP＝
；（2）见解析；（3）见解析.
【解析】
（1）设OA=a，OB=b，则a+b=8 ①，根据勾股定理可得b2+16=a2+4 ②，联立①②可求a，b的值，即可求OP的长；
（2）过点E作EF⊥AD于点F，证明四边形CDFE为矩形可得FE＝CD＝2，再根据CE＝1可得FE＝2CE.由此结论可证；
（3）分别过点C，B作CM⊥直线AD于点M，BN⊥直线AD于点N，根据角的二分线的定义可得BN=CM=2BC，通过证明四边形NBCM是矩形，可得∠NBC=∠MCB=90°，根据过直线外一点有且只有一条直线与已知直线垂直，可得点N与点A重合，点D与点M重合，可得四边形ABCD是矩形．
（1）设OA＝a，OB＝b，
则a+b＝8 ①，
∵PA⊥OA，PB⊥OB，
∴OP2＝OB2+BP2＝OA2+AP2，
∴b2+16＝a2+4 ②，
由①②组成方程组，
解得：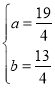
∴OP2＝OB2+BP2＝
∴OP＝
（2）如图，过点E作EF⊥AD于点F，
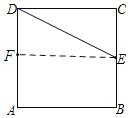
在正方形ABCD中，∠ADC＝∠C＝90°，
∴四边形CDFE为矩形，
∴FE＝CD＝2，
∵点E为BC中点，
∴CE＝1，
∴FE＝2CE，
∴DE是∠ADC的二分线
（3）如图，分别过点C，B作CM⊥直线AD于点M，BN⊥直线AD于点N，
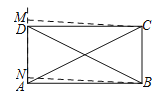
∵AB∥CD，∠ABC＝90°，
∴∠BCD＝90°，
∵AC是∠DAB二分线，
∴CM＝2BC，
∵BD是∠ADC的二分线，
∴BN＝2BC，
∴BN＝CM，
∵CM⊥AD，BN⊥AD，
∴BN∥CM，
∴四边形NBCM是平行四边形，
∵CM⊥AD，
∴四边形NBCM是矩形，
∴∠NBC＝∠MCB＝90°，
∴点N与点A重合，点D与点M重合，
∴四边形ABCD是矩形
