题目内容
2.(1)计算:$\sqrt{12}-4•sin60°+(-2)^{0}$(2)先化简,再求值:($\frac{1}{{x}^{2}-4}+\frac{1}{x+2}$)$÷\frac{{x}^{2}-2x+1}{{x}^{2}-4}$,其中x=-5.
分析 (1)分别根据数的开方法则、特殊角的三角函数值及0指数幂的运算法则计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=2$\sqrt{3}$-4×$\frac{\sqrt{3}}{2}$+1
=2$\sqrt{3}$-2$\sqrt{3}$+1
=1;
(2)原式=$\frac{1+x-2}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{{(x-1)}^{2}}$
=$\frac{1}{x-1}$,
当x=-5时,原式=$\frac{1}{-5-1}$=-$\frac{1}{6}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
12.下列语句:
①数轴上的点只能表示整数;
②数轴上的点只能表示有理数;
③数轴是一条直线;
④数轴上找不到既不表示正数,又不表示负数的点;
⑤所有理数都可以数轴上的点表示出来;
⑥数轴上的一个点只能表示一个数.
其中正确的有( )
①数轴上的点只能表示整数;
②数轴上的点只能表示有理数;
③数轴是一条直线;
④数轴上找不到既不表示正数,又不表示负数的点;
⑤所有理数都可以数轴上的点表示出来;
⑥数轴上的一个点只能表示一个数.
其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.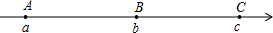 如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )
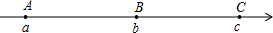 如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )| A. | 点A与点B之间靠近A点 | B. | 点A与点B之间靠近A点或点A的左边 | ||
| C. | 点B与点C之间靠近C点 | D. | 点B与点C之间靠近C点或点C的右边 |
17.下列各数中最小的数是( )
| A. | -3 | B. | 3 | C. | 0 | D. | -$\frac{1}{3}$ |
 如图,在正方形网格上的一个△ABC.以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出4个三角形与△ABC全等.
如图,在正方形网格上的一个△ABC.以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出4个三角形与△ABC全等.