Question

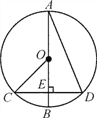
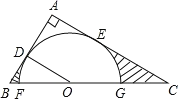
【题目】如图，在Rt△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连接OD，已知BD=2，AE=3，tan∠BOD=．

（1）求证：AE是 O的切线；

（2）求图中两部分阴影面积的和．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由AB为圆O的切线，利用切线的性质得到OD垂直于AB，在直角三角形BDO中，利用锐角三角函数定义，根据tan∠BOD及BD的值，求出OD的值；连接OE，由AE=OD=3，且OD与AE平行，利用一组对边平行且相等的四边形为平行四边形，根据平行四边形的对边平行得到OE与AD平行，再由DA与AE垂直得到OE与AC垂直，即可得证；

（2）阴影部分的面积由三角形BOD的面积+三角形ECO的面积-扇形DOF的面积-扇形EOG的面积，求出即可．

（1）∵AB与圆O相切，

∴OD⊥AB，

在Rt△BDO中，BD=2，tan∠BOD=，

∴OD=3；

连接OE.

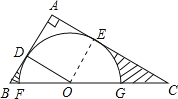
∵AB与圆O相切，

∴OD⊥AB.

∵在Rt△BDO中，BD=2，tan∠BOD=BDOD=23，

∴OD=3.

∵∠A=90°，OD⊥AB，

∴AE∥OD.

∵OD=AE=3，AE∥OD，

∴四边形AEOD为平行四边形，

∴AD∥EO.

∵DA⊥AE，

∴OE⊥AC.

又∵OE为圆的半径，

∴AC为圆O的切线.

（2）∵OD∥AC，

∴BD/BA=OD/CA，即=，

∴AC=7.5，

∴EC=AC-AE=7.5-3=4.5，

∴S阴影=S△BDO+S△OEC-(S扇形FOD+S扇形EOG)

=×2×3+×3×4.5-=3+-=.