题目内容
【题目】某学校要从数学竞赛初赛成绩相同的四名学生（其中2名男生，2名女生）中，随机选出2名学生去参加决赛，则选出的2名学生恰好为1名男生和1名女生的概率为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
设2名男生用1，2表示，2名女生用3，4表示，首先列举随机选出2名学生的基本事件，再列举出满足出的2名学生恰好为1名男生和1名女生的基本事件，根据古典概型的概率公式计算即可．
设2名男生用1，2表示，2名女生用3，4表示，随机选出2名学生的基本事件（1，2），（1，3），（1，4），（2，3），（2，4），（3，4）共6种，
选出的2名学生恰好为1名男生和1名女生的基本事件有（1，3），（1，4），（2，3），（2，4）共4种，
根据古典概率计算公式得选出的2名学生恰好为1名男生和1名女生的概率P=
．
故选C．
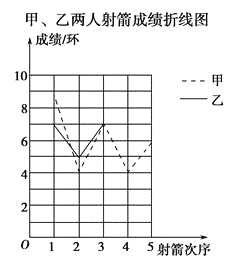
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩(单位：环)相同，小宇根据他们的成绩绘制了尚不完整的统计图表，并计算了甲成绩的平均数和方差(见小宇的作业)．
小宇的作业：
解：
甲＝
(9＋4＋7＋4＋6)＝6，
s甲2＝[(9－6)2＋(4－6)2＋(7－6)2＋(4－6)2＋(6－6)2]
＝(9＋4＋1＋4＋0)
＝3.6
小宇的作业：
解：甲＝(9＋4＋7＋4＋6)＝6，
s甲2＝[(9－6)2＋(4－6)2＋(7－6)2＋(4－6)2＋(6－6)2]
＝(9＋4＋1＋4＋0)
＝3.6
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a＝________，乙＝________；
(2)请完成图中表示乙成绩变化情况的折线；
(3)①观察图，可看出________的成绩比较稳定(填“甲”或“乙”)．参照小宇的计算方法，计算乙成绩的方差，并验证你的判断．
②请你从平均数和方差的角度分析，谁将被选中．
【题目】某市开展“环境治理留住青山绿水，绿色发展赢得金山银山”活动，对其周边的环境污染进行综合治理．
年对
、
两区的空气量进行监测，将当月每天的空气污染指数（简称：
）的平均值作为每个月的空气污染指数，并将年空气污染指数绘制如下表．据了解，空气污染指数
时，空气质量为优：
空气污染指数
时，空气质量为良：
空气污染指数
时，空气质量为轻微污染．
月份 地区 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）请求出、两区的空气污染指数的平均数；
（2）请从平均数、众数、中位数、方差等统计量中选两个对区、区的空气质量进行有效对比，说明哪一个地区的环境状况较好．
