题目内容
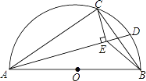
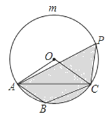
【题目】如图，在△ABC中，∠ABC=120°，⊙O是△ABC的外接圆，点P是
上的一个动点．
（1）求∠AOC的度数；
（2）若⊙O的半径为2，设点P到直线AC的距离为x，图中阴影部分的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围．\
【答案】（1）120°；（2）y=
﹣
+x（0≤x≤3）
【解析】
（1）先根据圆内接四边形的性质求出∠P的度数，再由圆周角定理即可得出结论；
（2）过点O作OH⊥AC于H，根据锐角三角函数的定义得出AH及OH的长，进而得出AC的长，用x表示出△APC的面积，再根据y=S扇形AOC-S△AOC+S△APC即可得出结论．
解：（1）∵∠ABC=120°，四边形ABCP是圆内接四边形，
∴∠P=180°﹣120°=60°，
∴∠AOC=2∠APC=120°；
（2）过点O作OH⊥AC于H，
∵∠AOC=120°，OC=OA=2，
∴∠OAC=30°，
∴AH=OAcos30°=2×
=，OH=
OA=1，
∴AC=2AH=2，
∴S△APC=ACx=x，
∴y=S扇形AOC﹣S△AOC+S△APC=
﹣×2×1+x=﹣+x（0≤x≤3）．
练习册系列答案
相关题目
【题目】某市开展“环境治理留住青山绿水，绿色发展赢得金山银山”活动，对其周边的环境污染进行综合治理．
年对
、
两区的空气量进行监测，将当月每天的空气污染指数（简称：
）的平均值作为每个月的空气污染指数，并将年空气污染指数绘制如下表．据了解，空气污染指数
时，空气质量为优：
空气污染指数
时，空气质量为良：
空气污染指数
时，空气质量为轻微污染．
月份 地区 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）请求出、两区的空气污染指数的平均数；
（2）请从平均数、众数、中位数、方差等统计量中选两个对区、区的空气质量进行有效对比，说明哪一个地区的环境状况较好．
