Question

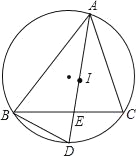
【题目】△ABC中，AB=CB，AC=10，S△ABC=60，E为AB上一动点，连结CE，过A作AF⊥CE于F，连结BF，则BF的最小值是_____．

Answer 1

【答案】7

【解析】

过B作BD⊥AC于D，根据S△ABC=60，计算BD的长，由∠AFC=90°，可知F在以AC为直径的圆上，由三角形三边关系得：BF+DF＞BD，则当F在BD上时，BF的值最小，求BF'的长即可.

解：过B作BD⊥AC于D，

∵AB=BC，

∴AD=CD=AC=5，

∵S△ABC=60，

∴ ×AC×BD＝60，即×10×BD＝60，

解得BD=12，

∵AF⊥CE，

∴∠AFC=90°，

∴F在以AC为直径的圆上，

∵BF+DF＞BD，且DF=DF'，

∴当F在BD上时，BF的值最小，

此时BF'=12-5=7，

则BF的最小值是7，

故答案为：7.