题目内容
17.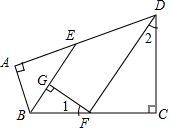 如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
分析 先根据四边形的内角和求出∠ADC+∠ABC=180°,再结合角平分线得出∠EBC+∠2=90°,再利用直角三角形的两锐角互余得出,∠1+∠EBC=90°,即可得出结论.
解答 解:∠1=∠2,
理由:∵∠A=∠C=90°,根据四边形的内角和得,∠ADC+∠ABC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠EBC=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ADC,
∴∠EBC+∠2=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ADC=90°,
∵FG⊥BE,
∴∠FGB=90°,
∴∠1+∠EBC=90°,
∴∠1=∠2.
点评 此题主要考查了四边形的内角和,角平分线的定义,直角三角形的性质,解本题的关键是整体求出∠EBC+∠2=90°.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
9.下列各题中,所求的最简公分母,错误的是( )
| A. | $\frac{1}{3x}$与$\frac{a}{6{x}^{2}}$最简公分母是6x2 | |
| B. | $\frac{1}{m+n}$与$\frac{1}{m-n}$的最简公分母是(m+n)(m-n) | |
| C. | $\frac{1}{3{a}^{2}{b}^{3}}$与$\frac{1}{3{a}^{2}{b}^{3}c}$最简公分母是3a2b3c | |
| D. | $\frac{1}{a(x-y)}$与$\frac{1}{b(y-x)}$的最简公分母是ab(x-y)(y-x) |
6.若点(-2,y1)、(-1,y2)、(1,y3)在反比例函数y=$\frac{2}{x}$的图象上,则下列结论中,正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
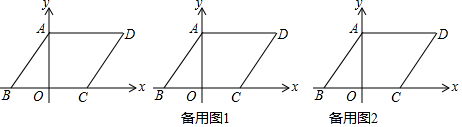
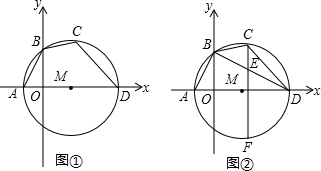
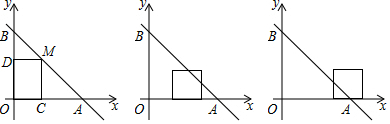
 将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.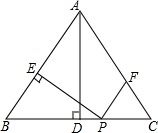 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.