题目内容
已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;
(2)如图②,当直线l与⊙O 相交于点E,F时,求证:∠DAE=∠BAF.
 |
1)证明:连接OC
在⊙O中,∵OA=OC
∴∠1=∠3
∵直线l与⊙O相切于点C
∴OC⊥l
∵AD⊥l
∴OC∥AD ∴∠3=∠2
∴∠1=∠2
∴AC平分∠DAB
 (2)证明:连接BF
(2)证明:连接BF
∵AB是⊙O的直径
∴∠AFB=90°
∴∠2+∠ABF=90°
∵AD⊥l ∴∠ADE=90°
∴∠1+∠AED=90°
∵AEFB内接于圆
∴∠AED=∠ABF
∴∠1=∠2 即:∠DAE=∠BAF

练习册系列答案
相关题目


 的部分图象如图所示,则下列结论中正确的是
的部分图象如图所示,则下列结论中正确的是 的解集是﹣1<x<5
的解集是﹣1<x<5

 ,
,
 证:OM=ON;
证:OM=ON;
 与AB之间的数量关系,并进行证明.
与AB之间的数量关系,并进行证明. (
( )的图象上,其中m,n 是方程
)的图象上,其中m,n 是方程 的两个根,则k的值是
的两个根,则k的值是 或
或 B.
B. 或
或 C.
C.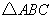 中,
中, ,以AC为直径的⊙O交AB于点D,E是BC的中点.
,以AC为直径的⊙O交AB于点D,E是BC的中点.