Question

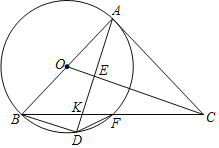
【题目】如图，在△ABC中，AB＝AC，∠BAC＝90°，以AB为直径的⊙O交BC于点F，连结OC，过点B作BD∥OC交⊙O点D．连接AD交OC于点E

（1）求证：BD＝AE．

（2）若OE＝1，求DF的值．

Answer 1

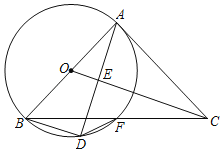
【答案】（1）见解析；（2）DF＝

【解析】

（1）由余角的性质可证∠BAD＝∠ACE，然后根据“AAS”证明△ADB≌△CEA，即可解决问题．

（2）由三角形的中位线可求BD的长，根据全等三角形的性质和垂径定理可求出AE、DE的长，根据勾股定理求出AB的长，根据平行线分线段成比例求出DK，进而求出BK，然后通过证明△AKB∽△FKD，利用相似三角形的性质求解即可解决问题．

（1）证明：∵AB是直径，

∴∠ADB＝90°，

∵BD∥OC，

∴∠AEO＝∠ADB＝90°，

∵∠OAC＝90°，

∴∠OAE+∠AOC＝90°，∠AOC+∠ACO＝90°，

∴∠BAD＝∠ACE，

∵AB＝AC，∠ADB＝∠AEC＝90°，

∴△ADB≌△CEA（AAS），

∴AE＝BD．

（2）∵OE∥BD，AO＝OB，

∴AE＝ED，

∴BD＝2OE＝2，

∴AE＝BD＝DE＝2，

∴AB＝＝2，

∵△ADB≌△CEA，

∴EC＝AD＝4，

设AD交BC于K．

∵EC∥BD，

∴＝＝2，

∴DK＝，

∴BK＝＝，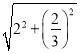

∵∠ABK＝∠FDK，∠AKB＝∠FKD，

∴△AKB∽△FKD，

∴＝，

∴＝，

∴DF＝．