题目内容
11．
如图，在△ABC中，AB＞AC，BC的垂直平分线DE分别交AB、BC于点D、E，AB=12cm，△ACD的周长为21cm，求AC的长．
分析 根据线段垂直平分线的性质，可得CD=BD，继而可得△ACD的周长为：AC+AB，则可求得答案．
解答 解：∵DE是BC的垂直平分线，
∴CD=BD，
∵AB=10cm，AC=6cm，
∴△ACD的周长为：AC+CD+AD=AC+AD+BD=AC+AB=AC+12=21，
∴AC=9．
点评 本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，有一个面积是120平方米的长方形养鸡场，鸡场的一边靠墙，墙长16米，与墙垂直的两侧均有一个1米宽的小门，除门外都用竹篱笆围成．若竹篱笆的总长30米，则鸡场的两邻边长各是多少？
如图，等腰三角形ABC中，BD=CD，AE=DE，求证：CF=2AF．
19．
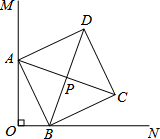如图，∠MON=90°，点B在射线ON上且OB=2，点A在射线OM上，以AB为边在∠MON内部作正方形ABCD，其对角线AC、BD交于点P．在点A从O点出发，沿射线OM的运动过程中，下列说法正确的是（ ）
如图，∠MON=90°，点B在射线ON上且OB=2，点A在射线OM上，以AB为边在∠MON内部作正方形ABCD，其对角线AC、BD交于点P．在点A从O点出发，沿射线OM的运动过程中，下列说法正确的是（ ）| A． | 点P始终在∠MON的平分线上，且线段OP的长有最小值等于$\sqrt{2}$ | |
| B． | 点P始终在∠MON的平分线上，且线段OP的长有最大值等于$\sqrt{2}$ | |
| C． | 点P不一定在∠MON的平分线上，但线段OP的长有最小值等于$\sqrt{2}$ | |
| D． | 点P运动路径无法确定 |