题目内容
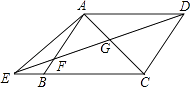
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
【答案】解:过点E、D分别作BC的垂线,交BC于点F、G.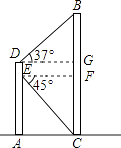
在Rt△EFC中,因为FC=AE=20,∠FEC=45°,
所以EF=20,
在Rt△DBG中,DG=EF=20,∠BDG=37°
因为tan∠BDG= ![]() ≈0.75,
≈0.75,
所以BG≈DG×0.75=20×0.75=15,
而GF=DE=5,
所以BC=BG+GF+FC=15+5+20=40.
答:大楼BC的高度是40米.
【解析】首先过点E、D分别作BC的垂线,交BC于点F、G,得两个直角三角形△EFC和△BDG,由已知大楼BC楼底C点的俯角为45°得出EF=FC=AE=20,DG=EF=20,再由直角三角形BDG,可求出BG,GF=DE=5,CO从而求出大楼的高度BC.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
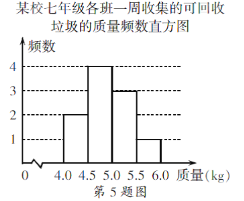
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.