题目内容
2.小明在初三复习归纳时发现初中阶段学习了三个非负数,分别是:①a2;②$\sqrt{a}$;③|a|(a是任意实数).于是他结合所学习的三个非负数的知识,自己编了一道题:已知(x+2)2+|x+y-1|=0,求xy的值.请你利用三个非负数的知识解答这个问题.分析 根据题意,可得(x+2)2+|x+y-1|=0,然后根据偶次方的非负性,以及绝对值的非负性,可得x+2=0,x+y-1=0,据此求出x、y的值各是多少,再把它们代入xy,求出xy的值是多少即可.
解答 解:∵(x+2)2+|x+y-1|=0,
∴$\left\{\begin{array}{l}{x+2=0}\\{x+y-1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,
∴xy=(-2)3=-8,
即xy的值是-8.
点评 (1)此题主要考查了偶次方的非负性,要熟练掌握,解答此题的关键是要明确:任意一个数的偶次方都是非负数,当几个数或式的偶次方相加和为0时,则其中的每一项都必须等于0.
(2)此题还考查了绝对值的非负性,要熟练掌握,解答此题的关键是要明确:任意一个数的绝对值都是非负数,当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0.
(3)此题还考查了一个数的乘方的求法,要熟练掌握.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | m3-m2=m | B. | -(-3)=3 | C. | (m+n)2=m2+n2 | D. | (3x)2=6x2 |
14.不等式2x-1>3的解集是( )
| A. | x>1 | B. | x<1 | C. | x>2 | D. | x<2 |
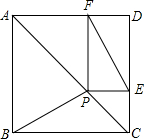 正方形ABCD中,点P是对角线AC上一点,PE⊥CD于E,PF⊥AD于F.
正方形ABCD中,点P是对角线AC上一点,PE⊥CD于E,PF⊥AD于F. 如图,已知∠BAC=∠BCA,∠BAE=∠BCD=90°,BE=BD.求证:∠E=∠D.
如图,已知∠BAC=∠BCA,∠BAE=∠BCD=90°,BE=BD.求证:∠E=∠D.