题目内容
14.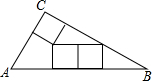 若三个边长为a的正方形按如图方式刚好能放在Rt△ABC内,则AB边的长为(2+2$\sqrt{3}$)a.
若三个边长为a的正方形按如图方式刚好能放在Rt△ABC内,则AB边的长为(2+2$\sqrt{3}$)a.
分析 连接AD,根据题意得∠DGH=90°,DG=a,DH=2a,根据直角三角形的性质得到∠DHG=30°,由于DH∥AB,得到∠B=30°,∠CAB=60°,通过Rt△ADE≌Rt△ADF,得到∠DAF=∠DAE=30°,于是求得AF=$\sqrt{3}$a,PF=2a,PB=$\sqrt{3}$a,则结论可得.
解答 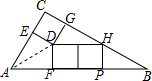 解:如图,连接AD,根据题意得:∠DGH=90°,DG=a,DH=2a,
解:如图,连接AD,根据题意得:∠DGH=90°,DG=a,DH=2a,
∴∠DHG=30°,
∵DH∥AB,
∴∠B=∠C=30°,
∴∠CAB=60°,
在Rt△ADE与Rt△ADF中,
$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$,
∴Rt△ADE≌Rt△ADF,
∴∠DAF=∠DAE=30°,
∴AF=$\sqrt{3}$a,PF=2a,PB=$\sqrt{3}$a,
∴AB=(2+2$\sqrt{3}$)a.
故答案为:(2+2$\sqrt{3}$)a.
点评 本题考查了正方形的性质,直角三角形的性质,全等三角形的判定和性质,熟练掌握直角三角形的性质是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
4. 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )| A. | 19° | B. | 29° | C. | 63° | D. | 73° |
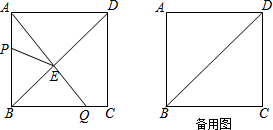
2.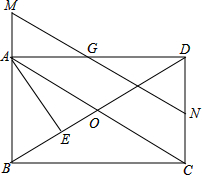 矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
 矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
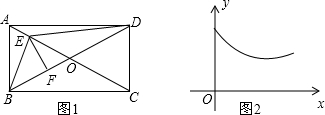
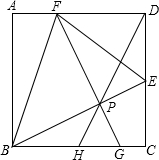 如图,点E,F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过点F作FG⊥BE于点P,交BC于点G,连接DP并延长交BC于点H,连接BF.EF.下列结论:
如图,点E,F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过点F作FG⊥BE于点P,交BC于点G,连接DP并延长交BC于点H,连接BF.EF.下列结论: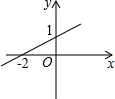 一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.
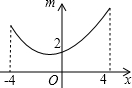
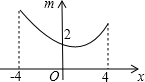
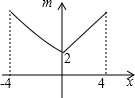
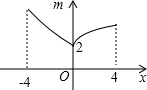
一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.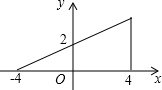 如图,若点P为函数y=kx+b(-4≤x≤4)图象上的一动点,m表示点P到原点O的距离,则下列图象中,能表示m与点P的横坐标x的函数关系的图象大致是( )
如图,若点P为函数y=kx+b(-4≤x≤4)图象上的一动点,m表示点P到原点O的距离,则下列图象中,能表示m与点P的横坐标x的函数关系的图象大致是( )