题目内容
在?ABCD中，E是AD的中点，若S?ABCD=1，则图中阴影部分的面积为
- A.
- B.
- C.
- D.
C
分析：可过点E、F作FG、EH垂直BC，利用平行线分线段成比例，求出△CBF与△BCE之间的关系，进而可求解阴影部分的面积．
解答：
解：过点E、F作FG、EH垂直BC，则FG∥EH，
∵E是AD的中点，若S?ABCD=1，
∴S△BCE=
S?ABCD=，
则S△CEF=S△BCE-S△BCF，
∵E是AD中点，四边形ABCD是平行四边形，
∴
=
，
又FG∥EH，
则
=
，
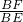
∴S△BCF=S△BCE，
∴S△CEF=S△BCE=×=．
故选C．
点评：本题主要考查平行四边形的性质及三角形面积的计算，能够利用平行线分线段成比例熟练解决此类问题．
分析：可过点E、F作FG、EH垂直BC，利用平行线分线段成比例，求出△CBF与△BCE之间的关系，进而可求解阴影部分的面积．
解答：
解：过点E、F作FG、EH垂直BC，则FG∥EH，∵E是AD的中点，若S?ABCD=1，
∴S△BCE=
S?ABCD=，则S△CEF=S△BCE-S△BCF，
∵E是AD中点，四边形ABCD是平行四边形，
∴
=，又FG∥EH，
则
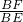
=，∴S△BCF=
S△BCE，∴S△CEF=
S△BCE=×=．故选C．
点评：本题主要考查平行四边形的性质及三角形面积的计算，能够利用平行线分线段成比例熟练解决此类问题．
练习册系列答案
阅读快车系列答案
相关题目
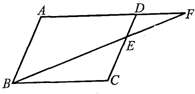9、如图，在?ABCD中，F是AD延长线上一点，连接BF交DC于点E，则图中相似三角形共有（ ）对．
如图，在?ABCD中，E是AB的中点，AF=3，则FC等于
如图，在?ABCD中，E是BC的中点，且∠AEC=∠DCE，下列结论中：
如图，在?ABCD中，E是BC上一点，AE交BD于F 已知BE：EC=3：1，S△FBE=18cm2，求S△FDA．
已知：如图，在?ABCD中，E是CD的中点，F是AE的中点，FC与BE交于G．