题目内容
2．已知方程x2+mx+3=0的两根是x1，x2，且x1+x2=4，则m的值是（ ）| A． | 4 | B． | -4 | C． | 3 | D． | -3 |
分析 由方程x2+mx+3=0的两根是x1，x2，且x1+x2=4，根据根与系数的关系可得-m=4，继而求得答案．
解答 解：∵方程x2+mx+3=0的两根是x1，x2，
∴x1+x2=-m，
∵x1+x2=4，
∴-m=4，
解得：m=-4．
故选B．
点评 此题考查了根与系数的关系．注意若二次项系数为1，常用以下关系：x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q．
练习册系列答案
相关题目
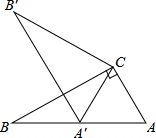如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为60°．
如图，抛物线y=（x+1）2+k与x轴交于A，B两点，与y轴交于点C（0，-3），抛物线的对称轴上存在一点P，使得PB+PC的值最小，求此时点P的坐标．
17．
如图1，在矩形MNPQ中，动点R从点N出发，沿着N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（ ）
如图1，在矩形MNPQ中，动点R从点N出发，沿着N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（ ）| A． | 当x=2时，y=5 | B． | 矩形MNPQ的面积是20 | ||
| C． | 当x=6时，y=10 | D． | 当y=$\frac{15}{2}$时，x=10 |
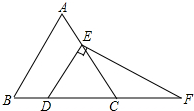如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．