题目内容
已知0°＜θ＜90°，且关于x的方程x2-2xtanθ-3=0的两个根的平方和等于10，则以tanθ，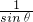
为根的一元二次方程为________．
y2-（1+
）y+=0
分析：首先利用根与系数的关系可以求出θ的度数，然后求出其它三角函数的值，再利用根与系数的关系即可求出方程形式．
解答：设x1，x2为关于x的方程x2-2xtanθ-3=0的两个根，
∴x1+x2=2tanθ，x1•x2=-3．
又∵x12+x22=10，
∴（x1+x2）2-2x1•x2=10，
∴4tan2θ+6=10，
∴tanθ=±1．
∵0°＜θ＜90°，
∴tanθ＞0，
∴tanθ=1，
∴θ=45度．
当θ=45°时，△=4tan2θ+12＞0，
∴tanθ+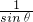=1+，
tanθ•=．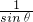
∴以tanθ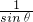，为根的一元二次方程为y2-（1+）y+=0．
故填空答案：y2-（1+）y+=0．
点评：本题解题关键：
1、一元二次方程的根与系数的关系x1+x2=-
、x1•x2=
来化简（x1+x2）2-2x1•x2=10；
2、特殊角的三角函数值要熟练．
）y+=0分析：首先利用根与系数的关系可以求出θ的度数，然后求出其它三角函数的值，再利用根与系数的关系即可求出方程形式．
解答：设x1，x2为关于x的方程x2-2xtanθ-3=0的两个根，
∴x1+x2=2tanθ，x1•x2=-3．
又∵x12+x22=10，
∴（x1+x2）2-2x1•x2=10，
∴4tan2θ+6=10，
∴tanθ=±1．
∵0°＜θ＜90°，
∴tanθ＞0，
∴tanθ=1，
∴θ=45度．
当θ=45°时，△=4tan2θ+12＞0，
∴tanθ+
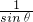=1+，tanθ•
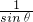=．∴以tanθ，
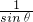为根的一元二次方程为y2-（1+）y+=0．故填空答案：y2-（1+
）y+=0．点评：本题解题关键：
1、一元二次方程的根与系数的关系x1+x2=-
、x1•x2=来化简（x1+x2）2-2x1•x2=10；2、特殊角的三角函数值要熟练．
练习册系列答案
阅读快车系列答案
相关题目
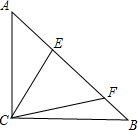如图，已知△ABC中，∠ACB=90°，AC=BC，点E、F在AB上，∠ECF=45°，若△ABC的面积为24，则AF•BE的值为（ ）| A、24 | ||
B、24
| ||
| C、36 | ||
| D、48 |
已知扇形的圆心角为90°，半径为2，则扇形的面积是（ ）
| A、π | ||
B、
| ||
| C、2π | ||
| D、4π |
如图，已知A1A2=1，∠OA1A2=90°，∠A1OA2=30°，以斜边OA2为直角边作直角三角形，使得∠A2OA3=30°，依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形，则A2A3=
